Advertisements
Advertisements
Question
In the following figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
Solution
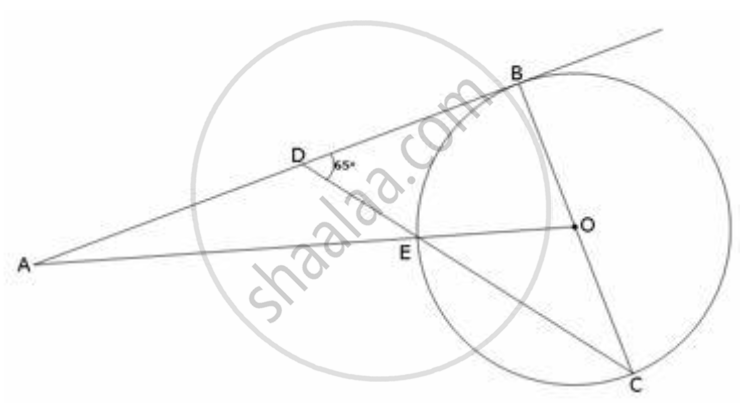
Form the given figure OB is the radius and therefore in triangle BDC
`∠DBC + ∠BDC + ∠BCD = 180^@`
`=> 90^@ + 65^@ + ∠BCD = 180^@`
=> ∠BCD = 25
Now, OE = OC = radius, ∠OEC = ∠OCE = 25° (as ∠OCE = ∠BCD)
=> ∠AED = ∠OEC = 25° (Vertically opposite angles)
Also, `∠ADE = 180^@ - 65^@ = 115^@`
Therefore in triangle AED
`∠BAO = 180^@ - 115^@ - 25^@ = 40^@`
APPEARS IN
RELATED QUESTIONS
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
If the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is 60°, then find the length of OP
In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions.
(1) What is the measure of ∠CAB ? Why ?
(2) What is the distance of point C from line AB? Why ?
(3) d(A,B) = 6 cm, find d(B,C).
(4) What is the measure of ∠ABC ? Why ? 
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
In fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = 5 cm, find PT.
Find the length of the tangent from a point which is at a distance of 5cm from the centre of the circle of radius 3cm.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find AB.

In the figure given below, PT is a tangent to the circle. Find PT if AT = 16 cm and AB = 12 cm.
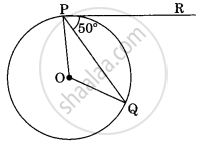
In figure, if O is the centre of a circle PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to ______.