Advertisements
Advertisements
Question
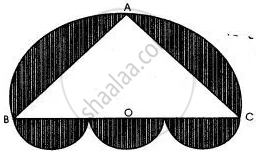
A doorway is decorated as shown in the figure. There are four semi-circles. BC, the diameter of the larger semi-circle is of length 84 cm. Centres of the three equal semicircles lie on BC. ABC is an isosceles triangle with AB = AC. If BO = OC, find the area of the shaded region. (Take `pi = 22/7`)
Solution 1
Here, the radius of larger semicircle = `84/2 = 42 cm`
And, the radius of smaller semi-circle = `84/(3xx2) = 14 cm`
Area of the shaded region =` (pi(42)^2)/2 + 3xx(pi(14)^2)/2 - 1/2 xx 84 xx 42`
`= 22/7 [21 xx 42 + 3 xx 14 xx 7] - 42 xx 42`
`= 22[3 xx 42 + 42] - 42 xx 42`
`= 42 xx [88 - 42]`
`= 1932 cm^2`
Solution 2
As angle in a semicircle is 90°,
∠ A = 90°
From Δ ABC,
by Pythagoras theorem, we get
AB2 + AC2 = BC2
⇒ x2 + x2 = 842
⇒ 2x2 = 84 x 84
⇒ x2 = 84 x 42
∴ Area of Δ ABC = `1/2` x AB x AC
= `1/2` x 84 cm x 42 cm
= 1764 cm2
Radius of semicircle with BC as diameter = `1/2` x 84 = 42 cm
Diameter of each of three equal semicircles = `1/3` x 84 = 28 cm
⇒ Radius of each of 3 equal semicircles = 14 cm
Area of the shaded region = Area of semicircle with 42 cm as Radius + Area of three equal semicircles of radius 14 cm - area of Δ ABC
= `1/2π xx 422 cm2 + 3 xx 1/2π xx 142 cm2 - 1764 cm2
= `1/2` π ( 422 + 3 xx 142 ) cm2 - 1764 cm2
= `1/2 xx 22/7` x 142 ( 9 + 3) cm2 - 1764 cm2
= 3696 cm2 - 1764 cm2 = 1932 cm2
APPEARS IN
RELATED QUESTIONS
A pendulum swings through an angle of 30º and describes an arc 8.8 cm in length. Find the length of the pendulum.
An arc of a circle is of length 5π cm and the sector it bounds has an area of 20 π cm2. Find the radius of the circle.
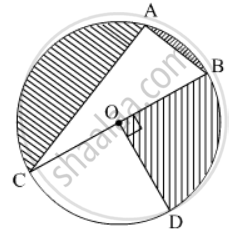
In the given figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of the shaded region.
Find the circumference of the circle with the following radius: (Take `bb(pi = 22/7`)
21 cm
Find the angle subtended at the centre of circle of radius 5cm by an arc of length `((5pi)/3)` cm
The minute hand of a clock is √21 𝑐𝑚 long. Find area described by the minute hand on the face of clock between 7 am and 7:05 am
In circle of radius 6cm, chord of length 10 cm makes an angle of 110° at the centre of circle find Area of the circle
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that
Area of shaded region is`r^2/2(tantheta −(pitheta)/180)`
The hypotenuse of a right-angled triangle is 65 cm and its base is 60 cm. Find the length of perpendicular and the area of the triangle.
The circumferences of two circles are in the ratio 2: 3. What is the ratio between their areas?
The length of a chain used as the boundary of a semicircular park is 108 m. Find the area of the park.
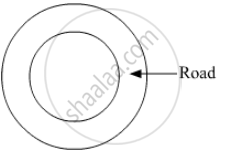
Diameter of the circular garden is 42 m. There is a 3.5 m wide road around the garden. Find the area of the road.
Find the curved surface area , the total surface area and the volume of a cone if its :
Height = 12 cm , radius = 5 cm
A circus tent is cylindrical to a height of 5 m and conical above it. If its diameter is 42 m and slant height of the cone is 53 m, calculate the total area of the canvas required.
The speed of the car is 66 km/hour. If each wheel of the car is 140 cm in diameter, find the number of revolutions made by each wheel per minute.
The circumference of a circular field is 308 m. Find is:
(i) Radius
(ii) Area.
The circumference of a circle is numerically equal to its area. Find the area and circumference of the circle.
A 4.2m wide road surrounds a circular plot whose circumference is 176m. Find the cost of paving the road at Rs.75per m2.
A wheel of a car covers a distance of 3520 cm in 20 rotations. Find the radius of the wheel?
Circumference ‘C’ of a circle can be found by multiplying diameter ‘d’ with ______.
