Advertisements
Advertisements
Question
A 4.2m wide road surrounds a circular plot whose circumference is 176m. Find the cost of paving the road at Rs.75per m2.
Solution
We know,
The area of the ring between two concentric circles equals the area of the larger circle minus the area of smaller circle.
Let the radius of the outer and inner ring be R and r respectively.
Here the circular garden is the inner circle and the 7m wide road is the ring
The Circumference of a Circle with radius r = 2πr
Here,
2πr = 176
⇒ r = `(176)/(2π)`
= `(176 xx 7)/(2 xx 22)`
= 28
⇒ r = 28m
⇒ R = 28 + 4.2
= 32.2m
inner Circle has radius r
= 28m and outer Circle has radius R
= 32.2m
π(32.22 - 282)
= `(22)/(7) xx (1036.84 - 784)`
= `(22)/(7) xx 252.84`
= 794.64m2
The cost of paving the road at the rate of Rs.150per m2
= 794.64 x 75
= Rs.59,598.
APPEARS IN
RELATED QUESTIONS
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that
Area of shaded region is`r^2/2(tantheta −(pitheta)/180)`
The circumferences of two circles are in the ratio 2: 3. What is the ratio between their areas?
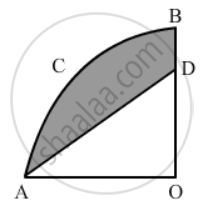
OACB is a quadrant of a circle with centre O and its radius is 3.5 cm. If OD = 2 cm. find the area of
- quadrant OACB
- the shaded region.
The circumference of a garden roller is 280 cm. How many revolutions does it make in moving 490 meters?
Construct an angle PQR = 45°. Mark a point S on QR such that QS = 4.5 cm. Construct a circle to touch PQ at Q and also to pass through S.
Find the area of a circular field that has a circumference of 396m.
Areas of two circles are equal. Is it necessary that their circumferences are equal? Why?
The radius of a circle whose circumference is equal to the sum of the circumferences of the two circles of diameters 36 cm and 20 cm is ______.
Circumference ‘C’ of a circle can be found by multiplying diameter ‘d’ with ______.
A circular pond is surrounded by a 2 m wide circular path. If outer circumference of circular path is 44 m, find the inner circumference of the circular path. Also find area of the path.
