Advertisements
Advertisements
Question
Two circles touch each other externally. The sum of their areas is 58πcm2 and the distance between their centres us 10cm. Find the radii of the two circles.
Solution
Let one of the two circles touching externally have a radius of R and the other have radius r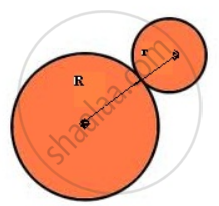
Given R + r = 10cm.
So, R = 10 - r
The Area of a Circle with radius r = πr2
The Area of a Circle with radius R = πR2
Sum of the areas of the two circles
= πr2 + πR
= π(r2 + R2)
= 58π
⇒ r2 + R2 = 58
⇒ r2 + (10 - r)2 = 58
⇒ r2 + 100 + r2 - 20r = 58
⇒ 2r2 - 20r + 42 = 0
⇒ r2 - 10r + 21 = 0
⇒ r2 - 7r - 3r + 21 = 0
⇒ r(r - 7) -3(r - 7) = 0
⇒ (r - 7)(r - 3) = 0
⇒ r = 7, 3
So, one of the two circles touching externally has a radius of 7cm and the other have radius 3cm.
APPEARS IN
RELATED QUESTIONS
The area of sector is one-twelfth that of the complete circle. Find the angle of the sector .
In the following figure, PQRS is a square of side 4 cm. Find the area of the shaded square.
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

If a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?
What is the area of a square inscribed in a circle of diameter p cm ?
The radius of a circle is 20 cm. It is divided into four parts of equal area by drawing three concentric circles inside it. Then, the radius of the largest of three concentric circles drawn is
In the given figure, O is the centre of the bigger circle, and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10, find the area of the shaded region.
The wheel of a cart is making 5 revolutions per second. If the diameter of the wheel is 84 cm, find its speed in km per hour.
The radii of two circles are in the ratio 5 : 8. If the difference between their areas is 156p cm2, find the area of the bigger circle.
