Advertisements
Advertisements
प्रश्न
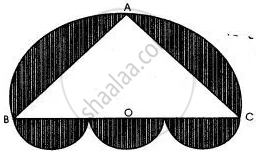
A doorway is decorated as shown in the figure. There are four semi-circles. BC, the diameter of the larger semi-circle is of length 84 cm. Centres of the three equal semicircles lie on BC. ABC is an isosceles triangle with AB = AC. If BO = OC, find the area of the shaded region. (Take `pi = 22/7`)
उत्तर १
Here, the radius of larger semicircle = `84/2 = 42 cm`
And, the radius of smaller semi-circle = `84/(3xx2) = 14 cm`
Area of the shaded region =` (pi(42)^2)/2 + 3xx(pi(14)^2)/2 - 1/2 xx 84 xx 42`
`= 22/7 [21 xx 42 + 3 xx 14 xx 7] - 42 xx 42`
`= 22[3 xx 42 + 42] - 42 xx 42`
`= 42 xx [88 - 42]`
`= 1932 cm^2`
उत्तर २
As angle in a semicircle is 90°,
∠ A = 90°
From Δ ABC,
by Pythagoras theorem, we get
AB2 + AC2 = BC2
⇒ x2 + x2 = 842
⇒ 2x2 = 84 x 84
⇒ x2 = 84 x 42
∴ Area of Δ ABC = `1/2` x AB x AC
= `1/2` x 84 cm x 42 cm
= 1764 cm2
Radius of semicircle with BC as diameter = `1/2` x 84 = 42 cm
Diameter of each of three equal semicircles = `1/3` x 84 = 28 cm
⇒ Radius of each of 3 equal semicircles = 14 cm
Area of the shaded region = Area of semicircle with 42 cm as Radius + Area of three equal semicircles of radius 14 cm - area of Δ ABC
= `1/2π xx 422 cm2 + 3 xx 1/2π xx 142 cm2 - 1764 cm2
= `1/2` π ( 422 + 3 xx 142 ) cm2 - 1764 cm2
= `1/2 xx 22/7` x 142 ( 9 + 3) cm2 - 1764 cm2
= 3696 cm2 - 1764 cm2 = 1932 cm2
APPEARS IN
संबंधित प्रश्न
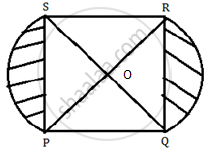
In the figure given below, PQRS is square lawn with side PQ = 42 metres. Two circular flower beds are there on the sides PS and QR with centre at O, the intersections of its
diagonals. Find the total area of the two flower beds (shaded parts).
The circumference of two circles are in ratio 2:3. Find the ratio of their areas
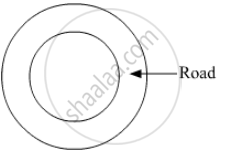
A road which is 7m wide surrounds a circular park whose circumference is 352m. Find the area of road.
Four equal circles each of radius a, touch each other. Show that area between them is `6/7a^2`
The radius of a sector of a circle is 7 cm. If the measure of the arc of the sector is - three right angles; find the area of the sector in case.
Choose the correct alternative answer for the following question.
The area of a circle is 49 π cm2. Its circumference is:
The area of a square is the same as the area of a square. Their perimeters are in the ratio
The diameter of a wheel is 84 cm. How many revolutions will it make to cover 792 m?
Diameter of the circular garden is 42 m. There is a 3.5 m wide road around the garden. Find the area of the road.
Find the curved surface area , the total surface area and the volume of a cone if its :
Height = 12 cm , radius = 5 cm
A conical tent with a capacity of 600 m3 stands on a circular base of area 160 m2 Find in m2 the area of the canvas.
A canvas tent is in the shape of a cylinder surmounted by a conical roof. The common diameter of the cone and the cylinder is 14 m. The height of the cylindrical part is 8 m and the height of the conical roof is 4 m. Find the area of the canvas used to make the tent.
Find the area grazed by a horse tied with a 11. 2 m rope to a corner of a field measuring 25m by 15 m.
Find the circumference of the circle whose area is 81π cm 2.
The wheel of the car makes 10 revolutions per second. If its diameter is 70 cm, find the speed of the car in km per hour.
The circumference of a given circular park is 55 m. It is surrounded by a path of uniform width of 3.5 m. Find the area of the path.
A circular racing track has inner circumference 528 m and outer circumference 616 m. Find the width of the track.
Find the area and perimeter of the circles with following: Diameter = 35cm
