Advertisements
Advertisements
प्रश्न
The figure shows a running track surrounding a grassed enclosure PQRSTU. The enclosure consists of a rectangle PQST with a semicircular region at each end, PQ = 200 m; PT = 70 meters.
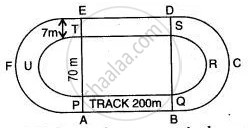
(i) Calculate the area of the grassed enclosure in m2.
(ii) Given that the track is of constant width 7 m, calculate the outer perimeter ABCDEF of the track. (Take π = `22/7`)
उत्तर
(i) Area of the grassed enclosure
= PQ x PT + `2 xx 1/2` x π x (35)2 ...( ∵ r = `70/2` = 35 m)
= 200 x 70 + `22/7` x 35 m x 35 m
= 14000 + 22 x 5 x 35 m2
= [ 14000 + 110 x 35 ] m2
= 14000 + 3850 = 17850 m2.
(ii) R = `[ (70 + 14)/2] "m" = 84/2 = 42 "m"`
Outer perimeter = 2I + 2 x `1/2` x 2πR
= 2 x 200 m + 2 x `22/7` x 42 m
= 400 m + 264 m
= 664 m.
APPEARS IN
संबंधित प्रश्न
A cylindrical tube of radius 12cm contains water to a depth of 20cm. A spherical ball is dropped into the tube and the level of the water is raised by 6.75cm.Find the radius of the ball .
A farmer runs a pipe of internal diameter 20 cm from the canal into a cylindrical tank in his field which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
If the radii of the circular ends of a conical bucket which is 45 cm high be 28 cm and 7 cm, find the capacity of the bucket. (Use π = 22/7).
A hollow sphere of external and internal diameters 8 cm and 4 cm, respectively is melted into a solid cone of base diameter 8 cm. Find the height of the cone.
Choose the correct answer of the following question:
A metallic solid sphere of radius 9 cm is melted to form a solid cylinder of radius 9 cm. The height of the cylinder is
A solid metallic sphere of diameter 21 cm is melted and recast into small cones of diameter 3.5 cm and height 3 cm each. Find the number of cones so formed.
A surahi is the combination of ______.
A cone of radius 8 cm and height 12 cm is divided into two parts by a plane through the mid-point of its axis parallel to its base. Find the ratio of the volumes of two parts.
A hemispherical bowl of internal radius 9 cm is full of liquid. The liquid is to be filled into cylindrical shaped bottles each of radius 1.5 cm and height 4 cm. How many bottles are needed to empty the bowl?
Water flows through a cylindrical pipe, whose inner radius is 1 cm, at the rate of 80 cm/sec in an empty cylindrical tank, the radius of whose base is 40 cm. What is the rise of water level in tank in half an hour?
