Advertisements
Advertisements
प्रश्न
A cone of radius 8 cm and height 12 cm is divided into two parts by a plane through the mid-point of its axis parallel to its base. Find the ratio of the volumes of two parts.
उत्तर
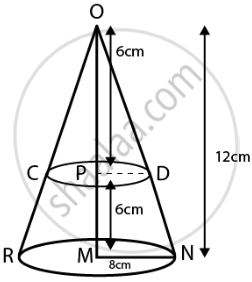
According to the question,
Height of cone = OM = 12 cm
The cone is divided from the mid-point.
Hence, let the mid-point of cone = P
OP = PM = 6 cm
From ΔOPD and ΔOMN
∠POD = ∠POD ...[Common]
∠OPD = ∠OMN ...[Both 90°]
Hence, by the Angle-Angle similarity criterion
We have,
ΔOPD ~ ΔOMN
And
Similar triangles have corresponding sides in equal ratio,
So, we have,
`"PD"/"MN" = "OP"/"OM"`
`"PD"/8 = 6/12`
PD = 4cm ...[MN = 8 cm = radius of base of cone]
For first part i.e. cone
Base radius, r = PD = 4 cm
Height, h = OP = 6 cm
We know that,
Volume of cone for radius r and height h, V = `1/3 π"r"^2"h"`
Volume of first part = `1/3 π(4)^(2)6` = 32π
For second part, i.e. Frustum
Bottom radius, r1 = MN = 8 cm
Top radius, r2 = PD = 4 cm
Height, h = PM = 6 cm
We know that,
Volume of frustum of a cone = `1/3 π"h"("r"_1^2 + "r"_2^2 + "r"_1"r"_2)`, where, h = height, r1 and r2 are radii, (r1 > r2)
Volume of second part = `1/3 π(6)[8^2 + 4^2 + 8(4)]`
= 2π(112)
= 224π
Therefore, we get the ratio,
Volume of first part : Volume of second part = 32π : 224π = 1 : 7
APPEARS IN
संबंधित प्रश्न
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
A spherical ball of radius 3cm is melted and recast into three spherical balls. The radii of the two of balls are 1.5cm and 2cm . Determine the diameter of the third ball?
Find the volume of the largest right circular cone that can be cut out of a cube where edgeis 9cm?
Rain water, which falls on a flat rectangular surface of length 6cm and breath 4m is
transferred into a cylindrical vessel of internal radius 20cm. What will be the height of
water in the cylindrical vessel if a rainfall of 1cm has fallen____?
A hollow sphere of internal and external diameter 4cm and 8cm is melted into a cone of base diameter 8cm. Calculate height of cone?
A hemispherical depression is cut out from one face of a cubical wooden block of edge 21 cm, such that the diameter of the hemisphere is equal to the edge of the cube. Determine the volume and total surface area of the remaining block.
A cylinder with base radius 8 cm and height 2 cm is melted to form a cone of height 6 cm. Calculate the radius of the base of the cone.
Three cubes of a metal whose edges are in the ratio 3 : 4 : 5 are melted and converted into a single cube whose diagonal is `12sqrt(3)` cm. Find the edges of the three cubes.
A cube of side 6 cm is cut into a number of cubes, each of side 2 cm. The number of cubes formed is
An iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of the base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find the weight of the pillar if one cubic cm of iron weight is 7.8 grams.
