Advertisements
Advertisements
प्रश्न
An iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of the base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find the weight of the pillar if one cubic cm of iron weight is 7.8 grams.
उत्तर
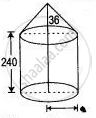
Let r1 cm and r2 cm denote the radii of the base of the cylinder and cone respectively. Then,
r1 = r2 = 8 cm
Let h1 and h2 cm be the height of the cylinder and the cone respectively. Then,
h1 = 240 cm and h2 = 36 cm.
Now, Volume of the cylinder = `πr_1^2h_1` cm3
= (π x 8 x 8 x 240 ) cm3
= (π x 64 x 240 ) cm3
Volume of the cone = `1/3 πr_2^2h_2` cm3
= `(1/3 π xx 8 xx 8 xx 36 )` cm3
= `(1/3 π xx 64 xx 36 )` cm3
∴ Total volume of iron = Volume of the cylinder + Volume of the cone
= `(π xx 64 xx 240 + 1/3 π xx 64 xx 36)` cm3
= ` π xx 64 xx (240 + 12)` cm3
= `22/7 xx 64 xx 252` cm3
= 22 x 64 x 36 cm3
Hence, total weight of the pillar = Volume x weight per cm3
= ( 22 x 64 x 36 ) x 7.8 gms
= 395366.4 gms
= 395.3664 kg.
APPEARS IN
संबंधित प्रश्न
A right circular cylinder having diameter 12 cm and height 15 cm is full ice-cream. The ice-cream is to be filled in cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
A metallic right circular cone 20cm high and whose vertical angle is 90° is cut into two parts at the middle point of its axis by a plane parallel to base. If frustum so obtained bee
drawn into a wire of diameter
(1/16) cm find length of the wire?
The radii of two cylinders are in the ratio 3 : 5. If their heights are in the ratio 2 : 3, then the ratio of their curved surface areas is
A cylindrical container of radius 6 cm and height 15 cm is filled with ice-cream. The whole ice-cream has to be distributed to 10 children in equal cones with hemispherical tops. If the height of the conical portion is 4 times the radius of its base, then find the radius of the ice-cream cone.
A spherical shell of lead, whose external and internal diameters are 24 cm and 18 cm, is melted and recast into a right circular cylinder 37 cm high. Find the diameter of the base of the cylinder.
A surahi is the combination of ______.
A rectangular water tank of base 11 m × 6 m contains water upto a height of 5 m. If the water in the tank is transferred to a cylindrical tank of radius 3.5 m, find the height of the water level in the tank.
A solid right circular cone of height 120 cm and radius 60 cm is placed in a right circular cylinder full of water of height 180 cm such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is equal to the radius of the cone.
Find the volume of a solid hemisphere whose total surface area is 462 sq.m.
A solid is in the shape of a hemisphere of radius 7 cm, surmounted by a cone of height 4 cm. The solid is immersed completely in a cylindrical container filled with water to a certain height. If the radius of the cylinder is 14 cm, find the rise in the water level.