Advertisements
Advertisements
प्रश्न
A metallic cylinder has a radius of 3 cm and a height of 5 cm. It is made of metal A. To reduce its weight, a conical hole is drilled in the cylinder, as shown and it is completely filled with a lighter metal B. The conical hole has a radius of `3/2` cm and its depth is `8/9` cm. Calculate the ratio of the volume of the metal A to the volume of metal B in the solid.
उत्तर
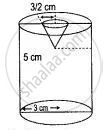
Volume of metal A = Volume of the cylinder - Volume of the cone
= `π (3)^2 x 5 - 1/3 π (3/2)^2 8/9`
= `π ( 45 - 2/3)`
= `133/3` π cm3
Volume of metal B = Volume of the conical cavity
= `1/3 xx (3/2)^2 . 8/9 = 2/3 π`
Hence, ratio of the volume of the metal A to the volume of the metal B.
= `(133/3 π)/(2/3 π) = 133/2`
= 66.5: 1.
APPEARS IN
संबंधित प्रश्न
A conical tent is 10 m high and the radius of its base is 24 m. Find
- slant height of the tent.
- cost of the canvas required to make the tent, if the cost of 1 m2 canvas is ₹ 70.
`["Assume "pi=22/7]`
A circus tent is cylindrical to a height of 3 meters and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m, calculate the length of the canvas 5 m
wide to make the required tent.
A cylinder and a cone have equal radii of their bases and equal heights. If their curved surface areas are in the ratio 8:5, show that the radius of each is to the height of each as 3:4.
Find the volume of a right circular cone with:
radius 6 cm, height 7 cm.
Find the volume of a right circular cone with:
height 21 cm and slant height 28 cm.
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilo litres?
Two right circular cone x and y are made x having three times the radius of y and y having half the volume of x. Calculate the ratio between the heights of x and y.
There are two cones. The curved surface area of one is twice that of the other. The slant height of the latter is twice that of the former. Find the ratio of their radii.
A vessel, in the form of an inverted cone, is filled with water to the brim. Its height is 32 cm and diameter of the base is 25.2 cm. Six equal solid cones are dropped in it, so that they are fully submerged. As a result, one-fourth of water in the original cone overflows. What is the volume of each of the solid cones submerged?
A hemispherical bowl of diameter 7.2 cm is filled completely with chocolate sauce. This sauce is poured into an inverted cone of radius 4.8 cm. Find the height of the cone if it is completely filled.
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres of radius 0.5 cm. Find the number of spheres formed.
A cone of height 15 cm and diameter 7 cm is mounted on a hemisphere of same diameter. Determine the volume of the solid thus formed.
A buoy is made in the form of hemisphere surmounted by a right cone whose circular base coincides with the plane surface of hemisphere. The radius of the base of the cone is 3.5 metres and its volume is two-third of the hemisphere. Calculate the height of the cone and the surface area of the buoy, correct to two places of decimal.
What will be the cost of making a closed cone of tin sheet having radius of base 6 m and slant height 8 m if the rate of making is Rs.10 per sq.m? `(π = 22/7)`
Volume of a cone is 1232 cm3 and its height is 24 cm. Find the surface area of the cone. `( π = 22/7)`
Find the height of the cone whose base radius is 5 cm and volume is 75π cm3.
Find the cost of painting a hemispherical dome of diameter 10 m at the rate of Rs 1.40 per square metre.
The circumference of the base of a 10 m high conical tent is 44 metres. Calculate the length of canvas used in making the tent if the width of the canvas is 2m. (Take π = 22/7)
A cloth having an area of 165 m2 is shaped into the form of a conical tent of radius 5 m. Find the volume of the cone.
