Advertisements
Advertisements
प्रश्न
A buoy is made in the form of hemisphere surmounted by a right cone whose circular base coincides with the plane surface of hemisphere. The radius of the base of the cone is 3.5 metres and its volume is two-third of the hemisphere. Calculate the height of the cone and the surface area of the buoy, correct to two places of decimal.
उत्तर
Radius of hemispherical part (r) = 3.5 m = `7/2 m`
Therefore, Volume of hemisphere = `2/3pir^3`
= `2/3 xx 22/7 xx 7/2 xx 7/2 xx 7/2`
= `539/6 m^3`
Volume of conical part = `2/3 xx 539/6 m^3` ...`(2/3 "of hemisphere")`
Let height of the cone = h
Then,
`1/3pir^2h = (2 xx 539)/(3 xx 6)`
`=> 1/3 xx 22/7 xx 7/2 xx 7/2 xx h = (2 xx 539)/(3 xx 6)`
`=> h =(2 xx 539 xx 2 xx 2 xx 7 xx 3)/(3 xx 6 xx 22 xx 7 xx 7)`
`=> h = 14/3m = 4 2/3m = 4.67 m`
Height of the cone = 4.67 m
Surface area of buoy = 2πr2 + πrl
But `l = sqrt(r^2 + h^2)`
`l = sqrt((7/2)^2 + (14/3)^2`
= `sqrt(49/4 + 196/9)`
= `sqrt(1225/36)`
= `35/6m`
Therefore, Surface area
= `(2 xx 22/7 xx 7/2 xx 7/2) + (22/7 xx 7/2 xx 35/6)m^2`
= `77/1 + 385/6`
= `847/6`
= 141.17 m2
Surface Area = 141.17 m2
APPEARS IN
संबंधित प्रश्न
A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is ₹ 12 per m2, what will be the cost of painting all these cones?
`("Use "π = 3.14" and take "sqrt1.04= 1.02)`
The radius of a cone is 5 cm and vertical height is 12 cm. Find the area of the curved surface.
The radius of a cone is 7 cm and area of curved surface is 176 `cm^2`. Find the slant height.
The height of a cone is 21 cm. Find the area of the base if the slant height is 28 cm.
Find the total surface area of a right circular cone with radius 6 cm and height 8 cm.
Find the curved surface area of a cone with base radius 5.25 cm and slant height 10cm.
The curved surface area of a cone is 4070 cm2 and its diameter is 70 cm. What is its slant height? (Use it 𝜋 = 22/7).
A conical tent is 10 m high and the radius of its base is 24 m. Find the slant height of the tent. If the cost of 1 2 m canvas is Rs. 70, find the cost of the canvas required to make the tent.
Find the volume of a right circular cone with:
radius 3.5 cm, height 12 cm
Two right circular cone x and y are made x having three times the radius of y and y having half the volume of x. Calculate the ratio between the heights of x and y.
There are two cones. The curved surface area of one is twice that of the other. The slant height of the latter is twice that of the former. Find the ratio of their radii.
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres of radius 0.5 cm. Find the number of spheres formed.
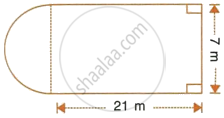
The horizontal cross-section of a water tank is in the shape of a rectangle with semi-circle at one end, as shown in the following figure. The water is 2.4 metres deep in the tank. Calculate the volume of water in the tank in gallons.
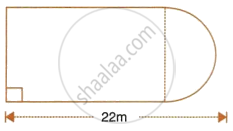
In the following diagram a rectangular platform with a semi-circular end on one side is 22 metres long from one end to the other end. If the length of the half circumference is 11 metres, find the cost of constructing the platform, 1.5 metres high at the rate of Rs. 4 per cubic metres.
A solid, consisting of a right circular cone standing one a hemisphere, is placed upright in a right circular cylinder, full of water, and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm; the radius of
the hemisphere is 2 cm and the height of cone is 4 cm. Give your answer to the nearest cubic centimeter.
Volume of a cone is 1232 cm3 and its height is 24 cm. Find the surface area of the cone. `( π = 22/7)`
The heights of two cones are in the ratio 1:3 and their base radii are in the ratio 3:1. Find the ratio of their volumes.
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown. Calculate: the total volume of the solid.
How many square metres of canvas is required for a conical tent whose height is 3.5 m and the radius of the base is 12 m?
