Advertisements
Advertisements
प्रश्न
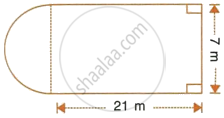
The horizontal cross-section of a water tank is in the shape of a rectangle with semi-circle at one end, as shown in the following figure. The water is 2.4 metres deep in the tank. Calculate the volume of water in the tank in gallons.
उत्तर
Length = 21 m
Depth of water = 2.4 m
Breadth = 7 m
Therefore, radius of semicircle = `7/2 m`
Area of cross-section = Area of rectangle + Area of semicircle
= `1 xx b + 1/2pir^2`
= `21 xx 7 + 1/2 xx 22/7 xx 7/2 xx 7/2`
= `147 + 77/4`
= `(588 + 77)/4`
= `665/4 m ^2`
Therefore, volume of water filled in gallons
= `665/4 xx 2.4 m^3`
= 665 × 0.6
= 399 m3
= 399 × 1003 cm3
= `(399 xx 100 xx 100 xx 100)/1000` gallons
= `(399 xx 100 xx 100 xx 100)/(1000 xx 4.5)`
= `(399 xx 100 xx 100 xx 100 xx 10)/(1000 xx 45 )` gallons
= `1330000/15` gallons
= `266000/3` gallons
= 88666.67 gallons
APPEARS IN
संबंधित प्रश्न
Find the curved surface area of a cone with base radius 5.25 cm and slant height 10cm.
A bus stop is barricated from the remaining part of the road, by using 50 hollow cones made of recycled card-board. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is Rs. 12 per m2, what will be the cost of painting all these cones. (Use 𝜋 = 3.14 and √1.04 = 1.02)
Find the volume of a right circular cone with:
radius 6 cm, height 7 cm.
The ratio of volumes of two cones is 4 : 5 and the ratio of the radii of their bases is 2:3. Find the ratio of their vertical heights.
A cylinder and a cone have equal radii of their bases and equal heights. Show that their volumes are in the ratio 3:1.
A right angled triangle of which the sides containing he right angle are 6.3 cm and lo cm in length, is made to turn round on the longer side. Find the volume of the solid, thus generated. Also, find its curved surface area.
The volume of a right circular cone is 9856 cm3. If the diameter of the base is 28 cm, find:
(i) height of the cone (ii) slant height of the cone (iii) curved surface area of the cone.
Monica has a piece of Canvas whose area is 551 m2. She uses it to have a conical tent made, with a base radius of 7m. Assuming that all the stitching margins and wastage incurred while cutting, amounts to approximately 1 m2. Find the volume of the tent that can be made with it.
Find the volume of a cone whose slant height is 17 cm and radius of base is 8 cm.
The radius and the height of a right circular cone are in the ratio 5 : 12 and its volume is 2512 cubic cm. Find the radius and slant height of the cone. (Take π = 3.14)
The total surface area of a right circular cone of slant height 13 cm is 90π cm2.
Calculate:
- its radius in cm.
- its volume in cm3. [Take π = 3.14].
A solid metallic cone, with radius 6 cm and height 10 cm, is made of some heavy metal A. In order to reduce its weight, a conical hole is made in the cone as shown and it is completely filled with a lighter metal B. The conical hole has a diameter of 6 cm and depth 4 cm. Calculate the ratio of the volume of metal A to the volume of the metal B in the solid.
What will be the cost of making a closed cone of tin sheet having radius of base 6 m and slant height 8 m if the rate of making is Rs.10 per sq.m? `(π = 22/7)`
Total surface area of a cone is 616 sq.cm. If the slant height of the cone is three times the radius of its base, find its slant height.
Find the radius of the circular base of the cone , if its volume is 154 cm3 and the perpendicular height is 12 cm
The heights of two cones are in the ratio 1:3 and their base radii are in the ratio 3:1. Find the ratio of their volumes.
The radius and height of a cylinder, a cone and a sphere are same. Calculate the ratio of their volumes.
Find the cost of painting a hemispherical dome of diameter 10 m at the rate of Rs 1.40 per square metre.
A conical tent is accommodate to 11 persons each person must have 4 sq. metre of the space on the ground and 20 cubic metre of air to breath. Find the height of the cone.
How many square metres of canvas is required for a conical tent whose height is 3.5 m and the radius of the base is 12 m?
