Advertisements
Advertisements
प्रश्न
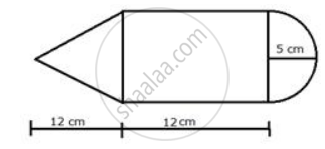
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown. Calculate: the total volume of the solid.
उत्तर
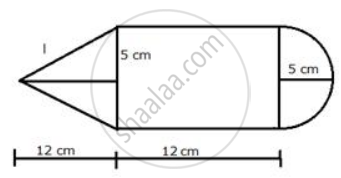
Diameter = 10 cm
Therefore, radius (r) = 5 cm
Height of the cone (h) = 12 cm
Height of the cylinder = 12 cm
`= 1/3 pi "r"^2"h" + pi"r"^2"h" + 2/3 pi "r"^3`
`= pi "r"^2 [1/3 "h" + "h" + 2/3 "r"]`
`= 22/7 xx 5 xx 5[1/3 xx 12 + 12 + 2/3 xx 5]`
`= 550/7 [4 + 12 + 10/3]`
`= 550/7 [16 + 10/3]`
`= 550/7 xx 58/3`
`= 31900/21`
= 1519.0476 cm3
APPEARS IN
संबंधित प्रश्न
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
`["Assume "pi=22/7]`
A joker’s cap is in the form of right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
`["Assume "pi=22/7]`
A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is ₹ 12 per m2, what will be the cost of painting all these cones?
`("Use "π = 3.14" and take "sqrt1.04= 1.02)`
Find the curved surface area of a cone, if its slant height is 60 cm and the radius of its base is 21 cm.
The radius of a cone is 7 cm and area of curved surface is 176 `cm^2`. Find the slant height.
The area of the curved surface of a cone is 60 cm2. If the slant height of the cone be 8 cm, find the radius of the base?
The diameters of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surfaces.
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of Rs. 210 per l00 m2.
If the radius of the base of a cone is halved, keeping the height same, what is the ratio of the volume of the reduced cone to that of the original cone?
A heap of wheat is in the form of a cone of diameter 9 m and height 3.5 m. Find its volume. How much canvas cloth is required to just cover the heap? (Use 𝜋 = 3.14).
Find the volume of the largest right circular cone that can be fitted in a cube whose edge is 14 cm.
The radius and the height of a right circular cone are in the ratio 5 : 12 and its volume is 2512 cubic cm. Find the radius and slant height of the cone. (Take π = 3.14)
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres of radius 0.5 cm. Find the number of spheres formed.
A cone and a hemisphere have the same base and the same height. Find the ratio between their volumes.
Find the curved surface area of a cone whose height is 8 cm and base diameter is 12 cm .
The radius and height of a cylinder, a cone and a sphere are same. Calculate the ratio of their volumes.
The total surface area of a right circular cone of slant height 13 cm is 90π cm2. Calculate: its volume in cm3. Take π = 3.14
Water flows at the rate of 10 m per minute through a cylindrical pipe 5 mm of diameter. How much time would it take to fill a conical vessel whose diameter at he surface is 40 cm and depth is 24 cm?
How many square metres of canvas is required for a conical tent whose height is 3.5 m and the radius of the base is 12 m?
