Advertisements
Advertisements
प्रश्न
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown.
Calculate :
- the total surface area.
- the total volume of the solid and
- the density of the material if its total weight is 1.7 kg.
उत्तर
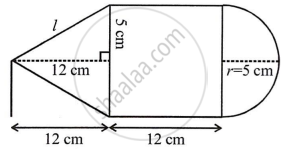
Diameter = 10 cm
Therefore, radius (r) = 5 cm
Height of the cone (h) = 12 cm
Height of the cylinder = 12 cm
∴ `l = sqrt(h^2 + r^2)`
= `sqrt(12^2 + 5^2)`
= `sqrt(144 + 25)`
= `sqrt(169)`
= 13 cm
i. Total surface area of the solid
= `pirl + 2pirh + 2pir^2`
= `pir(l + 2h + 2r)`
= `22/7 xx 5[13 + (2xx12) + (2 xx 5)]`
= `110/7 [13 + 24 + 10]`
= `110/7 xx 47`
= `5170/7`
= 738.57 cm2
ii. Total volume of the solid
= `1/3pir^2h + pir^2h + 2/3pir^3`
= `pir^2 [1/3h + h + 2/3r]`
= `22/7 xx 5 xx 5[1/3 xx 12 + 12 + 2/3 xx 5]`
= `550/7 [4 + 12 + 10/3]`
= `550/7 [16 + 10/3]`
= `550/7 xx 58/3`
= `31900/21`
= 1519.0476 cm3
iii. Total weight of the solid = 1.7 kg
∴ Density = `"Mass"/"Volume"`
= `(1.7 xx 1000)/(1519.0476)` gm/cm3
= `(17 xx 1000 xx 10000)/(10 xx 15190476)` gm/cm3
= 1.119 gm/cm3
`=>` Density = 1.12 gm/cm3
APPEARS IN
संबंधित प्रश्न
Find the surface area of a sphere of diameter 21 cm.
`["Assume "pi=22/7]`
Find the surface area of a sphere of diameter 3.5 m.
`["Assume "pi=22/7]`
The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
The surface area of a sphere is 2464 cm2, find its volume.
The volume of a sphere is 38808 cm3; find its diameter and the surface area.
Eight metallic spheres; each of radius 2 mm, are melted and cast into a single sphere. Calculate the radius of the new sphere.
If the number of square centimeters on the surface of a sphere is equal to the number of cubic centimeters in its volume, what is the diameter of the sphere?
A hollow sphere of internal and external diameter 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone.
A largest sphere is to be carved out of a right circular cylinder of radius 7 cm and height 14 cm. Find the volume of the sphere.
A solid is in the form of a cone standing on a hemi-sphere with both their radii being equal to 8 cm and the height of cone is equal to its radius. Find, in terms of π, the volume of the solid.
The cross-section of a tunnel is a square of side 7 m surmounted by a semi-circle as shown in the adjoining figure. The tunnel is 80 m long.
Calculate:
- its volume,
- the surface area of the tunnel (excluding the floor) and
- its floor area.

The total surface area of a hemisphere of radius r is
If the surface area of a sphere is 144π m2, then its volume (in m3) is
Find the surface area and volume of sphere of the following radius. (π = 3.14)
4 cm
The internal and external diameters of a hollow hemi-spherical vessel are 21 cm and 28 cm respectively. Find volume of material of the vessel.
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find: the weight of the material drilled out if it weighs 7 gm per cm3.
A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area.
Find the volume and surface area of a sphere of diameter 21 cm.
The radius of a sphere is 10 cm. If we increase the radius 5% then how many % will increase in volume?
