Advertisements
Advertisements
प्रश्न
The internal and external diameters of a hollow hemi-spherical vessel are 21 cm and 28 cm respectively. Find volume of material of the vessel.
उत्तर
External radius (R) = 14 cm
Internal radius (r) = `21/2` cm
`2/3pi(R^3 - r^3)`
= `2/3 xx 22/7((14)^3 - (21/2)^3)`
= `44/21(2744 - 1157.625)`
= `44/21 xx 1586.375`
= `3323.83 "cm"^3`
APPEARS IN
संबंधित प्रश्न
Find the surface area of a sphere of diameter 21 cm.
`["Assume "pi=22/7]`
The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres of radius 0.5 cm. Find the number of spheres formed.
If the number of square centimeters on the surface of a sphere is equal to the number of cubic centimeters in its volume, what is the diameter of the sphere?
The surface area of a solid sphere is increased by 12% without changing its shape. Find the percentage increase in its:
- radius
- volume
Find the volume of a sphere whose surface area is 154 cm2.
Mark the correct alternative in each of the following:
In a sphere the number of faces is
A sphere and a cube are of the same height. The ratio of their volumes is
If the ratio of volumes of two spheres is 1 : 8, then the ratio of their surface areas is
A sphere is placed inside a right circular cylinder so as to touch the top, base and lateral surface of the cylinder. If the radius of the sphere is r, then the volume of the cylinder is
A cone and a hemisphere have equal bases and equal volumes the ratio of their heights is
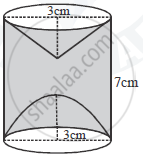
A hemispherical and a conical hole is scooped out of a.solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows:
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm.
Give your answer correct to the nearest whole number.Taken`pi = 22/7`.
Find the radius of a sphere whose surface area is equal to the area of the circle of diameter 2.8 cm
Find the radius of the sphere whose surface area is equal to its volume .
A solid metallic cylinder has a radius of 2 cm and is 45 cm tall. Find the number of metallic spheres of diameter 6 cm that can be made by recasting this cylinder .
A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area.
There is a ratio 1: 4 between the surface area of two spheres, find the ratio between their radius.
The radius of a sphere is 10 cm. If we increase the radius 5% then how many % will increase in volume?
A spherical ball of radius 3 cm is melted and recast into three spherical balls. The radii of two of the balls are 1.5 cm and 2 cm. Find the diameter of the third ball.
