Advertisements
Advertisements
प्रश्न
The surface area of a solid sphere is increased by 12% without changing its shape. Find the percentage increase in its:
- radius
- volume
उत्तर
Let the radius of the sphere be 'r'.
Total surface area the sphere, S = 4πr2
New surface area of the sphere, S’
= `4pir^2 + 21/100 xx 4pir^2`
= `121/100 4pir^2`
i. Let the new radius be r1
`S^I = 4pir_1^2`
`S^I = 121/100 4pir^2`
`=> 4pir_1^2 = 121/100 4pir^2`
`=> r_1^2 = 121/100r^2`
`=> r_1 = 11/10r`
`=> r_1 = r + r/10`
`=> r_1 - r = r/10`
`=>` Change in radius = `r/10`
Percentage change in radius = `"Change in radius"/"Original in radius" xx 100`
= `(r/10)/r xx 100`
= 10
Percentage change in radius = 10%
ii. Let the volume of the sphere be V
Let the new volume of the sphere be V'.
`V = 4/3pir^3`
`V^I = 4/3pir_1^3`
`=> V^I = 4/3pi((11r)/10)^3`
`=> V^I = 4/3pi1331/1000 r^3`
`=> V^I = 4/3pir^3 1331/1000 `
`=> V^I = 1331/1000 V`
`=> V^I = V + 1331/1000 V`
`=> V^I - V = 331/1000 V`
∴ Change in volume = `331/1000 V `
Percentage change in volume = `"Change in volume"/"Original volume" xx 100`
= `(331/1000V)/V xx 100`
= `331/10`
= 33.1
Percentage change in volume = 33.1%
APPEARS IN
संबंधित प्रश्न
The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
Two solid spheres of radii 2 cm and 4 cm are melted and recast into a cone of height 8 cm. Find the radius of the cone so formed.
Find the surface area of a sphere of radius 10.5 cm .
Find the surface area of a sphere of diameter 21 cm .
A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin- plating
it on the inside at the rate of Rs. 4 per 100 `cm^2`
Assuming the earth to be a sphere of radius 6370 km, how many square kilo metres is area
of the land, if three-fourth of the earth’s surface is covered by water?
The diameter of the moon is approximately one fourth of the diameter of the earth. Find the
ratio of their surface areas.
A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast.
A hollow sphere of internal and external radii 6 cm and 8 cm respectively is melted and recast into small cones of base radius 2 cm and height 8 cm. Find the number of cones.
Find the radius of a sphere whose surface area is 154 cm2.
The hollow sphere, in which the circus motor cyclist performs his stunts, has a diameter of 7 m. Find the area available to the motorcyclist for riding.
If a sphere of radius 2r has the same volume as that of a cone with circular base of radius r, then find the height of the cone.
Mark the correct alternative in each of the following:
In a sphere the number of faces is
If the ratio of volumes of two spheres is 1 : 8, then the ratio of their surface areas is
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. The ratio of their volumes is
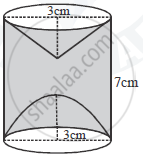
A hemispherical and a conical hole is scooped out of a.solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows:
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm.
Give your answer correct to the nearest whole number.Taken`pi = 22/7`.
Find the surface area and volume of sphere of the following radius. (π = 3.14)
4 cm
Find the surface area and volume of sphere of the following radius. (π = 3.14 )
9 cm
Find the surface area and volume of sphere of the following radius. (π = 3.14 )
3.5 cm
How many lead balls of radii 1 cm each can be made from a sphere of 8 cm radius?
