Advertisements
Advertisements
प्रश्न
Find the surface area and volume of sphere of the following radius. (π = 3.14 )
3.5 cm
उत्तर
Radius of the sphere, r = 3.5 cm
Surface area of the sphere = 4 πr2
= 4 × 3.14 × (3.5)2
= 153.86 cm2
Volume of the sphere = `4/3`πr3
= `4/3 xx 3.14 xx (3.5)^3`
= 179.50 cm3
APPEARS IN
संबंधित प्रश्न
The dome of a building is in the form of a hemisphere. Its radius is 63 dm. Find the cost of
painting it at the rate of Rs. 2 per sq. m.
A largest sphere is to be carved out of a right circular cylinder of radius 7 cm and height 14 cm. Find the volume of the sphere.
The total surface area of a hemisphere of radius r is
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find: the weight of the material drilled out if it weighs 7 gm per cm3.
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown.
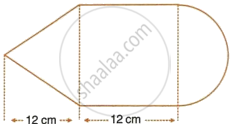
Calculate :
- the total surface area.
- the total volume of the solid and
- the density of the material if its total weight is 1.7 kg.
A spherical cannon ball, 28 cm in diameter is melted and recast into a right circular conical mould, the base of which is 35 cm in diameter. Find the height of the cone, correct to one place of decimal.
A sphere cut out from a side of 7 cm cubes. Find the volume of this sphere?
A vessel is in he form of an inverted cone. Its height is 11 cm., and the radius of its top which is open is 2.5 cm. It is filled with water up to the rim. When lead shots, each of which is a sphere of radius 0.25 cm., are dropped 2 into the vessel, `2/5`th of the water flows out. Find the number of lead shots dropped into the vessel.
The radius of a sphere is 10 cm. If we increase the radius 5% then how many % will increase in volume?
A manufacturing company prepares spherical ball bearings, each of radius 7 mm and mass 4 gm. These ball bearings are packed into boxes. Each box can have maximum of 2156 cm3 of ball bearings. Find the:
- maximum number of ball bearings that each box can have.
- mass of each box of ball bearings in kg.
(use π = `22/7`)
