Advertisements
Advertisements
प्रश्न
Find the volume of a sphere whose surface area is 154 cm2.
Advertisements
उत्तर
In the given problem, we have to find the volume of a sphere whose surface area is given.
So, let us first find the radius of the given sphere.
Surface area of the sphere (S) = 154 cm2
Let the radius of the sphere be r cm
Now, we know that surface area of the sphere = `4pir^2`
So,
`154 = 4(22/7)(r)^2`
` r^2 = ((154)(7))/((4)(22))`
` r^2 = 12.25`
Further, solving for r
`r = sqrt(12.25)`
r= 3.5
Therefore, the radius of the given sphere is 3.5 cm.
Now, the volume of the sphere = `4/3 pi r^3`
`=(4/3)(22/7)(3.5)^3`
=179.66 cm2
Therefore, the volume of the given sphere is 179.66 cm2 .
APPEARS IN
संबंधित प्रश्न
Find the surface area of a sphere of diameter 14 cm.
`["Assume "pi=22/7]`
A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of ₹ 16 per 100 cm2.
`["Assume "pi=22/7]`
Find the total surface area of a hemisphere and a solid hemisphere each of radius 10 cm.
(Use 𝜋 = 3.14)
Assuming the earth to be a sphere of radius 6370 km, how many square kilo metres is area
of the land, if three-fourth of the earth’s surface is covered by water?
A hemi-spherical dome of a building needs to be painted. If the circumference of the base of
the dome is 17.6 cm, find the cost of painting it, given the cost of painting is Rs. 5 per l00
`cm^2`
Metallic spheres of radii 6 cm, 8 cm and 10 cm respectively are melted and recasted into a single solid sphere. Taking π = 3.1, find the surface area of the solid sphere formed.
A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast.
A hollow sphere of internal and external diameter 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone.
The total surface area of a hemisphere of radius r is
The ratio of the total surface area of a sphere and a hemisphere of same radius is
If a sphere is inscribed in a cube, then the ratio of the volume of the sphere to the volume of the cube is
If a solid sphere of radius r is melted and cast into the shape of a solid cone of height r, then the radius of the base of the cone is
A solid metallic cylinder has a radius of 2 cm and is 45 cm tall. Find the number of metallic spheres of diameter 6 cm that can be made by recasting this cylinder .
The internal and external diameters of a hollow hemi-spherical vessel are 21 cm and 28 cm respectively. Find volume of material of the vessel.
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown.
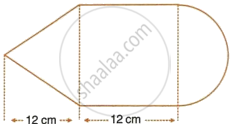
Calculate :
- the total surface area.
- the total volume of the solid and
- the density of the material if its total weight is 1.7 kg.
Find the volume and surface area of a sphere of diameter 21 cm.
There is surface area and volume of a sphere equal, find the radius of sphere.
The radius of two spheres are in the ratio of 1 : 3. Find the ratio between their volume.
The cylinder of radius 12 cm have filled the 20 cm with water. One piece of iron drop in the stands of water goes up 6.75 cm. Find the radius of sphere piece.
A manufacturing company prepares spherical ball bearings, each of radius 7 mm and mass 4 gm. These ball bearings are packed into boxes. Each box can have a maximum of 2156 cm3 of ball bearings. Find the:
- maximum number of ball bearings that each box can have.
- mass of each box of ball bearings in kg.
(Use π = `22/7`)
