Advertisements
Advertisements
प्रश्न
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres of radius 0.5 cm. Find the number of spheres formed.
उत्तर
A volume of solid cone = `1/3 pir^2h = 1/3 xx 22/7 xx 5^2 xx 8 = 1/3 xx 22/7 xx 25 xx 8`
Volume of a small sphere = `4/3 pir^3 = 4/3 xx 22/7 xx (5/10)^3 = 4/3 xx 22/7 xx 125/1000`
Number of spheres formed = `"Volumeof cone"/"Volumeof sphere"` = `(1/3 xx 22/7 xx 25xx8)/(4/3 xx 22/7 xx 125/1000) = 400`
Thus 400 spheres are obtained by melting the solid cone.
APPEARS IN
संबंधित प्रश्न
Find the surface area of a sphere of diameter 21 cm.
`["Assume "pi=22/7]`
A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of ₹ 16 per 100 cm2.
`["Assume "pi=22/7]`
On a map drawn to a scale of 1: 50,000, a rectangular plot of land ABCD has the following dimensions. AB = 6 cm; BC = 8 cm and all angles are right angles. Find:
1) the actual length of the diagonal distance AC of the plot in km.
2) the actual area of the plot in sq. km.
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate:
- the radius of the sphere.
- the number of cones recast. (Take π = `22/7`)
Find the surface area of a sphere of diameter 3.5 cm .
A hemi-spherical dome of a building needs to be painted. If the circumference of the base of
the dome is 17.6 cm, find the cost of painting it, given the cost of painting is Rs. 5 per l00
`cm^2`
How many balls each of radius 1 cm can be made by melting a bigger ball whose diameter is 8 cm?
A solid rectangular block of metal 49 cm by 44 cm by 18 cm is melted and formed into a solid sphere. Calculate the radius of the sphere.
A solid is in the form of a cone standing on a hemi-sphere with both their radii being equal to 8 cm and the height of cone is equal to its radius. Find, in terms of π, the volume of the solid.
If a sphere of radius 2r has the same volume as that of a cone with circular base of radius r, then find the height of the cone.
If a sphere is inscribed in a cube, find the ratio of the volume of cube to the volume of the sphere.
If the ratio of volumes of two spheres is 1 : 8, then the ratio of their surface areas is
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. The ratio of their volumes is
The radius of a sphere is 9 cm. It is melted and drawn into a wire of diameter 2 mm. Find the length of the wire in metre.
Find the length of the wire of diameter 4 m that can be drawn from a solid sphere of radius 9 m.
The total area of a solid metallic sphere is 1256 cm2. It is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate: the number of cones recasted [π = 3.14]
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown.
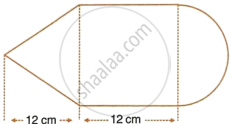
Calculate :
- the total surface area.
- the total volume of the solid and
- the density of the material if its total weight is 1.7 kg.
A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area.
How many spherical bullets can be made out of a solid cube of lead whose edge measures 44 cm, each bullet being 4 cm in diameter?
The internal and external diameters of a hollow hemispherical vessel are 20 cm and 28 cm respectively. Find the cost to paint the vessel all over at ₹ 0.14 per cm2
