Advertisements
Advertisements
Question
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown.
Calculate :
- the total surface area.
- the total volume of the solid and
- the density of the material if its total weight is 1.7 kg.
Advertisements
Solution
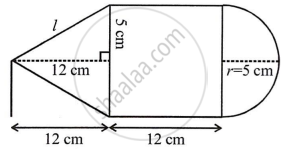
Diameter = 10 cm
Therefore, radius (r) = 5 cm
Height of the cone (h) = 12 cm
Height of the cylinder = 12 cm
∴ `l = sqrt(h^2 + r^2)`
= `sqrt(12^2 + 5^2)`
= `sqrt(144 + 25)`
= `sqrt(169)`
= 13 cm
i. Total surface area of the solid
= `pirl + 2pirh + 2pir^2`
= `pir(l + 2h + 2r)`
= `22/7 xx 5[13 + (2xx12) + (2 xx 5)]`
= `110/7 [13 + 24 + 10]`
= `110/7 xx 47`
= `5170/7`
= 738.57 cm2
ii. Total volume of the solid
= `1/3pir^2h + pir^2h + 2/3pir^3`
= `pir^2 [1/3h + h + 2/3r]`
= `22/7 xx 5 xx 5[1/3 xx 12 + 12 + 2/3 xx 5]`
= `550/7 [4 + 12 + 10/3]`
= `550/7 [16 + 10/3]`
= `550/7 xx 58/3`
= `31900/21`
= 1519.0476 cm3
iii. Total weight of the solid = 1.7 kg
∴ Density = `"Mass"/"Volume"`
= `(1.7 xx 1000)/(1519.0476)` gm/cm3
= `(17 xx 1000 xx 10000)/(10 xx 15190476)` gm/cm3
= 1.119 gm/cm3
`=>` Density = 1.12 gm/cm3
RELATED QUESTIONS
Find the surface area of a sphere of diameter 21 cm.
`["Assume "pi=22/7]`
A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin- plating
it on the inside at the rate of Rs. 4 per 100 `cm^2`
The diameter of the moon is approximately one fourth of the diameter of the earth. Find the
ratio of their surface areas.
Eight metallic spheres; each of radius 2 mm, are melted and cast into a single sphere. Calculate the radius of the new sphere.
The total surface area of a hemisphere of radius r is
A sphere is placed inside a right circular cylinder so as to touch the top, base and lateral surface of the cylinder. If the radius of the sphere is r, then the volume of the cylinder is
A hemispherical bowl of internal radius 9 cm is full of liquid. This liquid is to be filled into conical shaped small containers each of diameter 3 cm and height 4 cm. How many containers are necessary to empty the bowl?
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate : the number of cones recast. `("Take" pi =22/7)`
A spherical cannon ball, 28 cm in diameter is melted and recast into a right circular conical mould, the base of which is 35 cm in diameter. Find the height of the cone, correct to one place of decimal.
The cylinder of radius 12 cm have filled the 20 cm with water. One piece of iron drop in the stands of water goes up 6.75 cm. Find the radius of sphere piece.
