Advertisements
Advertisements
प्रश्न
Volume of a cone is 1232 cm3 and its height is 24 cm. Find the surface area of the cone. `( π = 22/7)`
उत्तर
Let the radius of the base and slant height of the cone be r cm and lcm, respectively.
Height of the cone, h = 24 cm
Volume of the cone = 1232 cm3
∴ `1/3`πr2h = 1232 cm3
∴ `1232 = 1/3 × 22/7 × r^2 × 24`
⇒ `(1232xx3xx7)/(22xx24) = r^2 ...("Multiplying both sides by" 3xx7/22xx1/24)`
⇒ r2 = 49
⇒ r = `sqrt(49)`
⇒ r = 7 cm
Now,
l2 = r2 + h2
⇒ l2 = (7)2 + (24)2
⇒ l2 = 49 + 576
⇒ l2 = 625
⇒ l = `sqrt 625`
⇒ l = 25 cm
∴ Curved Surface area of the cone = πrl
= `22/7 xx 7 xx 25`
= 550 cm2
Thus, the surface area of the cone is approximately 550 cm2.
Notes
There is a printing mistake in the textbook, the Volume of a cone is 1232 cm3 instead of 1212 cm3
APPEARS IN
संबंधित प्रश्न
Curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find
- radius of the base and
- total surface area of the cone.
`["Assume "pi =22/7]`
Find the volume of the largest right circular cone that can be fitted in a cube whose edge is 14 cm.
A buoy is made in the form of hemisphere surmounted by a right cone whose circular base coincides with the plane surface of hemisphere. The radius of the base of the cone is 3.5 metres and its volume is two-third of the hemisphere. Calculate the height of the cone and the surface area of the buoy, correct to two places of decimal.
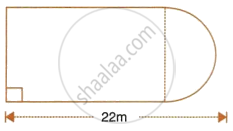
In the following diagram a rectangular platform with a semi-circular end on one side is 22 metres long from one end to the other end. If the length of the half circumference is 11 metres, find the cost of constructing the platform, 1.5 metres high at the rate of Rs. 4 per cubic metres.
Find the height of the cone whose base radius is 5 cm and volume is 75π cm3.
The total surface area of a right circular cone of slant height 13 cm is 90π cm2. Calculate: its volume in cm3. Take π = 3.14
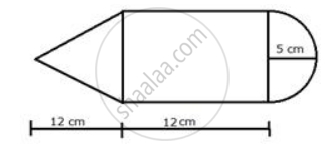
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown. Calculate: the density of the material if its total weight is 1.7 kg
The circumference of the base of a 10 m high conical tent is 44 metres. Calculate the length of canvas used in making the tent if the width of the canvas is 2m. (Take π = 22/7)
Water flows at the rate of 10 m per minute through a cylindrical pipe 5 mm of diameter. How much time would it take to fill a conical vessel whose diameter at he surface is 40 cm and depth is 24 cm?
How many square metres of canvas is required for a conical tent whose height is 3.5 m and the radius of the base is 12 m?
