Advertisements
Advertisements
प्रश्न
A conical tent is 10 m high and the radius of its base is 24 m. Find
- slant height of the tent.
- cost of the canvas required to make the tent, if the cost of 1 m2 canvas is ₹ 70.
`["Assume "pi=22/7]`
उत्तर
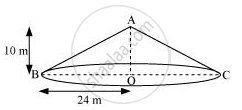
(i) Let ABC be a conical tent.
Height (h) of conical tent = 10 m
Radius (r) of conical tent = 24 m
Let the slant height of the tent be l.
In ΔABO,
AB2 = AO2 + BO2
l2 = h2 + r2
= (10 m)2 + (24 m)2
= 676 m2
∴ l = 26 m
Therefore, the slant height of the tent is 26 m.
(ii) Curved surface area of the tent = πrl
= `(22/7xx24xx26)m^2`
= `13728/7 m^2`
Cost of 1 m2 canvas = ₹ 70
`"Cost of "13728/7 m^2 " canvas"` = `₹ (13728/7xx70)`
= ₹ 137280
Therefore, the cost of the canvas required to make such a tent is ₹ 137280.
APPEARS IN
संबंधित प्रश्न
Find the ratio of the curved surface areas of two cones if their diameters of the bases are equal and slant heights are in the ratio 4 : 3.
Curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find the radius of the base and total surface area of the cone.
The ratio of volumes of two cones is 4 : 5 and the ratio of the radii of their bases is 2:3. Find the ratio of their vertical heights.
A heap of wheat is in the form of a cone of diameter 9 m and height 3.5 m. Find its volume. How much canvas cloth is required to just cover the heap? (Use 𝜋 = 3.14).
Find the volume of a cone whose slant height is 17 cm and radius of base is 8 cm.
The curved surface area of a cone is 12320 cm2. If the radius of its base is 56 cm, find its height.
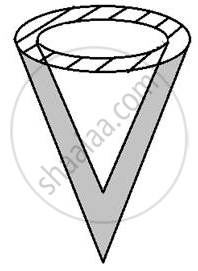
A solid metallic cone, with radius 6 cm and height 10 cm, is made of some heavy metal A. In order to reduce its weight, a conical hole is made in the cone as shown and it is completely filled with a lighter metal B. The conical hole has a diameter of 6 cm and depth 4 cm. Calculate the ratio of the volume of metal A to the volume of the metal B in the solid.
A cone and a hemisphere have the same base and the same height. Find the ratio between their volumes.
Find the curved surface area of a cone whose height is 8 cm and base diameter is 12 cm .
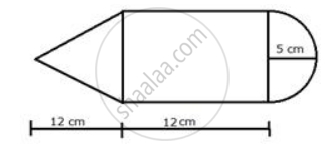
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown. Calculate: the density of the material if its total weight is 1.7 kg