Advertisements
Advertisements
प्रश्न
What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm. [Use π = 3.14]
उत्तर
Height (h) of conical tent = 8 m
Radius (r) of base of tent = 6 m
Slant height (l) of tent = `sqrt(r^2+h^2)`
= `sqrt(6^2+8^2) m`
= `sqrt100 m`
= 10 m
The curved surface area of conical tent = πrl
= (3.14 × 6 × 10) m2
= `314/100 xx 6 xx 10 m^2`
= 188.4 m2
Let the length of the tarpaulin sheet required be l.
As 20 cm will be wasted, therefore, the effective length will be (l − 0.2 m).
Breadth of tarpaulin = 3 m
Area of sheet = Curved surface area of the tent
[(l − 0.2 m) × 3] m = 188.4 m2
l − 0.2 m = 62.8 m
l = 63 m
Therefore, the length of the required tarpaulin sheet will be 63 m.
APPEARS IN
संबंधित प्रश्न
Find the volume of a right circular cone with:
radius 6 cm, height 7 cm.
The radius and the height of a right circular cone are in the ratio 5 : 12 and its volume is 2512 cubic cm. Find the radius and slant height of the cone. (Take π = 3.14)
The diameter of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surface areas.
The total surface area of a right circular cone of slant height 13 cm is 90π cm2.
Calculate:
- its radius in cm.
- its volume in cm3. [Take π = 3.14].
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find :
- the surface area of remaining solid,
- the volume of remaining solid,
- the weight of the material drilled out if it weighs 7 gm per cm3.
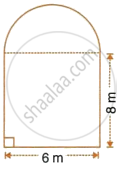
The cross-section of a railway tunnel is a rectangle 6 m broad and 8 m high surmounted by a semi-circle as shown in the figure. The tunnel is 35 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs. 2.25 per m2.
The ratio of the base area and the curved surface of a conical tent is 40: 41. If the height is 18 m, Find the air capacity of the tent in terms of n.
The radius and height of cone are in the ratio 3 : 4. If its volume is 301.44 cm3. What is its radius? What is its slant height? (Take π = 3.14)
The curved surface area of a right circular cone of height 15 cm and base diameter 16 cm is
A cloth having an area of 165 m2 is shaped into the form of a conical tent of radius 5 m. Find the volume of the cone.
