Advertisements
Advertisements
प्रश्न
What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm. [Use π = 3.14]
उत्तर
Height (h) of conical tent = 8 m
Radius (r) of base of tent = 6 m
Slant height (l) of tent = `sqrt(r^2+h^2)`
= `sqrt(6^2+8^2) m`
= `sqrt100 m`
= 10 m
The curved surface area of conical tent = πrl
= (3.14 × 6 × 10) m2
= `314/100 xx 6 xx 10 m^2`
= 188.4 m2
Let the length of the tarpaulin sheet required be l.
As 20 cm will be wasted, therefore, the effective length will be (l − 0.2 m).
Breadth of tarpaulin = 3 m
Area of sheet = Curved surface area of the tent
[(l − 0.2 m) × 3] m = 188.4 m2
l − 0.2 m = 62.8 m
l = 63 m
Therefore, the length of the required tarpaulin sheet will be 63 m.
APPEARS IN
संबंधित प्रश्न
The diameters of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surfaces.
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of Rs. 210 per l00 m2.
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres of radius 0.5 cm. Find the number of spheres formed.
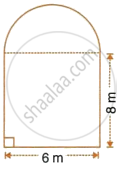
The cross-section of a railway tunnel is a rectangle 6 m broad and 8 m high surmounted by a semi-circle as shown in the figure. The tunnel is 35 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs. 2.25 per m2.
A solid, consisting of a right circular cone standing one a hemisphere, is placed upright in a right circular cylinder, full of water, and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm; the radius of
the hemisphere is 2 cm and the height of cone is 4 cm. Give your answer to the nearest cubic centimeter.
Volume of a cone is 1232 cm3 and its height is 24 cm. Find the surface area of the cone. `( π = 22/7)`
Find the height of the cone whose base radius is 5 cm and volume is 75π cm3.
The volume of a conical tent is 1232 m3 and the area of the base floor is 154 m2. Calculate the: length of the canvas required to cover this conical tent if its width is 2 m.
A vessel in the form of an inverted cone is filled with water to the brim: Its height is 20 cm and the diameter is 16.8 cm. Two equal solid cones are dropped in it so that they are fully submerged. As a result, one-third of the water in the original cone overflows. What is the volume of each of the solid cones submerged?
How many square metres of canvas is required for a conical tent whose height is 3.5 m and the radius of the base is 12 m?
