Advertisements
Advertisements
प्रश्न
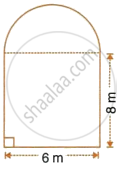
The cross-section of a railway tunnel is a rectangle 6 m broad and 8 m high surmounted by a semi-circle as shown in the figure. The tunnel is 35 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs. 2.25 per m2.
उत्तर
Breadth of the tunnel = 6 m
Height of the tunnel = 8 m
Length of the tunnel = 35 m
Radius of the semi-circle = 3 m
Circumference of the semi-circle = πr
= `22/7 xx 3`
= `66/7` m
Internal surface area of the tunnel
= `35(8 + 8 + 66/7)`
= `35(16 + 66/7)`
= `35((112 + 66)/7)`
= `35 xx 178/7`
= 890 m2
Rate of plastering the tunnel = Rs. 2.25 per m2
Therefore, total expenditure = Rs. `890xx225/100`
= `890 xx 9/4`
= `8010/4`
= Rs. 2002.5
APPEARS IN
संबंधित प्रश्न
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of ₹ 210 per 100 m2.
`["Assume "pi=22/7]`
A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is ₹ 12 per m2, what will be the cost of painting all these cones?
`("Use "π = 3.14" and take "sqrt1.04= 1.02)`
Find the curved surface area of a cone with base radius 5.25 cm and slant height 10cm.
A conical tent is 10 m high and the radius of its base is 24 m. Find the slant height of the tent. If the cost of 1 2 m canvas is Rs. 70, find the cost of the canvas required to make the tent.
A cylinder and a cone have equal radii of their bases and equal heights. If their curved surface areas are in the ratio 8:5, show that the radius of each is to the height of each as 3:4.
Find the volume of a right circular cone with:
height 21 cm and slant height 28 cm.
The radius and height of a right circular cone are in the ratio 5 : 12 and its volume is 2512 cubic cm. Find the slant height and radius of the cone. (Use it 𝜋 = 3.14).
The ratio of volumes of two cones is 4 : 5 and the ratio of the radii of their bases is 2:3. Find the ratio of their vertical heights.
Two right circular cone x and y are made x having three times the radius of y and y having half the volume of x. Calculate the ratio between the heights of x and y.
The diameter of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surface areas.
A hemispherical bowl of diameter 7.2 cm is filled completely with chocolate sauce. This sauce is poured into an inverted cone of radius 4.8 cm. Find the height of the cone if it is completely filled.
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres of radius 0.5 cm. Find the number of spheres formed.
Find the height of the cone whose base radius is 5 cm and volume is 75π cm3.
A sphere and a cone have the same radii. If their volumes are also equal, prove that the height of the cone is twice its radius.
Find the cost of painting a hemispherical dome of diameter 10 m at the rate of Rs 1.40 per square metre.
A hollow metallic cylindrical tube has an internal radius of 3.5 cm and height 21 cm. The thickness of the metal tube is 0.5 cm. The tube is melted and cast into a right circular cone of height 7 cm. Find the radius of the cone, correct to one decimal place.
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown. Calculate: the total volume of the solid.
The circumference of the base of a 10 m high conical tent is 44 metres. Calculate the length of canvas used in making the tent if the width of the canvas is 2m. (Take π = 22/7)
Water flows at the rate of 10 m per minute through a cylindrical pipe 5 mm of diameter. How much time would it take to fill a conical vessel whose diameter at he surface is 40 cm and depth is 24 cm?
The ratio of the radii of two right circular cones of the same height is 1 : 3. Find the ratio of their curved surface area when the height cone is 3 times the radius of the smaller cone.
