Advertisements
Advertisements
प्रश्न
A hemispherical bowl of diameter 7.2 cm is filled completely with chocolate sauce. This sauce is poured into an inverted cone of radius 4.8 cm. Find the height of the cone if it is completely filled.
उत्तर
Diameter of the hemispherical bowl = 7.2 cm
Therefore, radius = 3.6 cm
Volume of sauce in hemispherical bowl = `2/3pir^3`
= `2/3pi xx (3.6)^3`
Radius of the cone = 4.8 cm
Volume of cone = `1/3pir^2h`
= `1/3pi xx (4.8)^2 xx h`
Now, volume of sauce in hemispherical bowl = volume of cone
`=> 2/3pi xx (3.6)^3 = 1/3pi xx (4.8)^2 xx h`
`=> h = (2 xx 3.6 xx 3.6 xx 3.6)/(4.8 xx 4.8)`
`=>` h = 4.05 cm
Height of the cone = 4.05 cm
APPEARS IN
संबंधित प्रश्न
The curved surface area of a cone is 4070 cm2 and its diameter is 70 cm. What is its slant height? (Use it 𝜋 = 22/7).
There are two cones. The curved surface area of one is twice that of the other. The slant height of the later is twice that of the former. Find the ratio of their radii.
The ratio of volumes of two cones is 4 : 5 and the ratio of the radii of their bases is 2:3. Find the ratio of their vertical heights.
A heap of wheat is in the form of a cone of diameter 9 m and height 3.5 m. Find its volume. How much canvas cloth is required to just cover the heap? (Use 𝜋 = 3.14).
A heap of wheat is in the form of a cone of diameter 9 m and height 3.5 m. Find its volume. How much canvas cloth is required to just cover the heap? (Use 𝜋 = 3.14).
A right angled triangle of which the sides containing he right angle are 6.3 cm and lo cm in length, is made to turn round on the longer side. Find the volume of the solid, thus generated. Also, find its curved surface area.
A solid metallic cone, with radius 6 cm and height 10 cm, is made of some heavy metal A. In order to reduce its weight, a conical hole is made in the cone as shown and it is completely filled with a lighter metal B. The conical hole has a diameter of 6 cm and depth 4 cm. Calculate the ratio of the volume of metal A to the volume of the metal B in the solid.
A cubical block of side 7 cm is surmounted by a hemisphere of the largest size. Find the surface area of the resulting solid.
The radii of the bases of two solid right circular cones of same height are r1 and r2 respectively. The cones are melted and recast into a solid sphere of radius R. Find the height of each cone in terms r1, r2 and R.
A cone and a hemisphere have the same base and the same height. Find the ratio between their volumes.
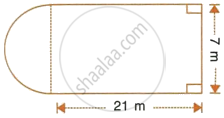
The horizontal cross-section of a water tank is in the shape of a rectangle with semi-circle at one end, as shown in the following figure. The water is 2.4 metres deep in the tank. Calculate the volume of water in the tank in gallons.
A solid, consisting of a right circular cone standing one a hemisphere, is placed upright in a right circular cylinder, full of water, and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm; the radius of
the hemisphere is 2 cm and the height of cone is 4 cm. Give your answer to the nearest cubic centimeter.
A solid is in the form of a right circular cone mounted on a hemisphere. The diameter of the base of the cone, which exactly coincides with hemisphere, is 7 cm and its height is 8 cm. The solid is placed in a cylindrical vessel of internal radius 7 cm and height 10 cm. How much water, in cm3, will be required to fill the vessel completely?
Total surface area of a cone is 616 sq.cm. If the slant height of the cone is three times the radius of its base, find its slant height.
Find the volume of the right circular cone whose height is 12 cm and slant length is 15 cm . (π = 3.14)
A sphere and a cone have the same radii. If their volumes are also equal, prove that the height of the cone is twice its radius.
The volume of a conical tent is 1232 m3 and the area of the base floor is 154 m2. Calculate the: length of the canvas required to cover this conical tent if its width is 2 m.
The surface area of a solid sphere is increased by 21% without changing its shape. Find the percentage increase in its: volume
