Advertisements
Advertisements
प्रश्न
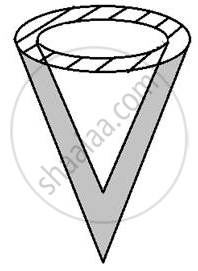
A solid metallic cone, with radius 6 cm and height 10 cm, is made of some heavy metal A. In order to reduce its weight, a conical hole is made in the cone as shown and it is completely filled with a lighter metal B. The conical hole has a diameter of 6 cm and depth 4 cm. Calculate the ratio of the volume of metal A to the volume of the metal B in the solid.
उत्तर
Volume of the whole cone of metal A
= `1/3pir^2h`
= `1/3 xx pi xx 6^2 xx 10`
= 120π
Volume of the cone with metal B
= `1/3pir^2h`
= `1/3 xx pi xx 3^2 xx 4`
= 12π
Final volume of cone with metal A
= 120π – 12π
= 108π
`"Volume of cone with metal A"/"Volume of cone with metal B"`
= `(108pi)/(12pi)`
= `9/1`
APPEARS IN
संबंधित प्रश्न
The radius of a cone is 5 cm and vertical height is 12 cm. Find the area of the curved surface.
The curved surface area of a cone is 4070 cm2 and its diameter is 70 cm. What is its slant height? (Use it 𝜋 = 22/7).
A conical tent is 10 m high and the radius of its base is 24 m. Find the slant height of the tent. If the cost of 1 2 m canvas is Rs. 70, find the cost of the canvas required to make the tent.
A right angled triangle of which the sides containing he right angle are 6.3 cm and lo cm in length, is made to turn round on the longer side. Find the volume of the solid, thus generated. Also, find its curved surface area.
The volume of a right circular cone is 9856 cm3. If the diameter of the base is 28 cm, find:
(i) height of the cone (ii) slant height of the cone (iii) curved surface area of the cone.
The curved surface area of a cone is 12320 cm2. If the radius of its base is 56 cm, find its height.
The circumference of the base of a 12 m high conical tent is 66 m. Find the volume of the air contained in it.
The area of the base of a conical solid is 38.5 cm2 and its volume is 154 cm3. Find the curved surface area of the solid.
Total volume of three identical cones is the same as that of a bigger cone whose height is 9 cm and diameter 40 cm. Find the radius of the base of each smaller cone, if height of each is 108 cm
A cubical block of side 7 cm is surmounted by a hemisphere of the largest size. Find the surface area of the resulting solid.
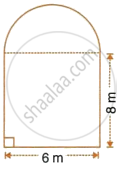
The cross-section of a railway tunnel is a rectangle 6 m broad and 8 m high surmounted by a semi-circle as shown in the figure. The tunnel is 35 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs. 2.25 per m2.
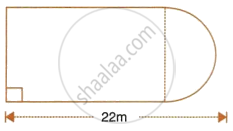
In the following diagram a rectangular platform with a semi-circular end on one side is 22 metres long from one end to the other end. If the length of the half circumference is 11 metres, find the cost of constructing the platform, 1.5 metres high at the rate of Rs. 4 per cubic metres.
The curved surface area of a cone is 2200 sq.cm and its slant height is 50 cm. Find the total surface area of cone. `(π = 22/7)`
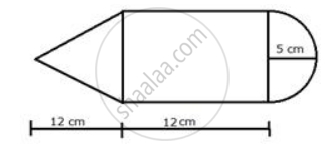
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown. Calculate: the density of the material if its total weight is 1.7 kg
The ratio of the base area and the curved surface of a conical tent is 40: 41. If the height is 18 m, Find the air capacity of the tent in terms of n.
The radius and height of cone are in the ratio 3 : 4. If its volume is 301.44 cm3. What is its radius? What is its slant height? (Take π = 3.14)
A conical tent is accommodate to 11 persons each person must have 4 sq. metre of the space on the ground and 20 cubic metre of air to breath. Find the height of the cone.
The ratio of the radii of two right circular cones of the same height is 1 : 3. Find the ratio of their curved surface area when the height cone is 3 times the radius of the smaller cone.
A cloth having an area of 165 m2 is shaped into the form of a conical tent of radius 5 m. Find the volume of the cone.
