Advertisements
Advertisements
प्रश्न
A solid is in the form of a right circular cone mounted on a hemisphere. The diameter of the base of the cone, which exactly coincides with hemisphere, is 7 cm and its height is 8 cm. The solid is placed in a cylindrical vessel of internal radius 7 cm and height 10 cm. How much water, in cm3, will be required to fill the vessel completely?
उत्तर
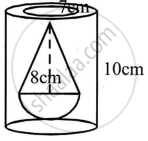
Diameter of hemisphere = 7 cm
Diameter of the base of the cone = 7 cm
Therefore, radius (r) = 3.5 cm
Height (h) = 8 cm
Volume of the solid = `1/3pir^2h + 2/3pir^3`
= `1/3pir^2(h + 2r)`
= `1/3 xx 22/7 xx 3.5 xx 3.5(8 + 2 xx 3.5)`
= `77/6(8 + 7)`
= `385/2`
= 192.5 cm3
Now, radius of cylindrical vessel (R) = 7 cm
Height (H) = 10 cm
∴ Volume = πR2h
= `22/7 xx 7 xx 7 xx 10`
= 1540 cm3
Volume of water required to fill
= 1540 – 192.5
= 1347.5 cm3
APPEARS IN
संबंधित प्रश्न
Find the curved surface area of a cone with base radius 5.25 cm and slant height 10cm.
The area of the curved surface of a cone is 60 cm2. If the slant height of the cone be 8 cm, find the radius of the base?
What length of tarpaulin 3 m wide will be required to make a conical tent of height 8 m and base radius 6 m? Assume that the extra length of material will be required for stitching margins and wastage in cutting is approximately 20 cm (Use it 𝜋 = 3.14)
The radius and the height of a right circular cone are in the ratio 5 : 12. If its volume is 314 cubic meter, find the slant height and the radius (Use it 𝜋 = 3.14).
A cylinder and a cone have equal radii of their bases and equal heights. Show that their volumes are in the ratio 3:1.
A heap of wheat is in the form of a cone of diameter 9 m and height 3.5 m. Find its volume. How much canvas cloth is required to just cover the heap? (Use 𝜋 = 3.14).
The diameter of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surface areas.
A heap of wheat is in the form of a cone of diameter 16.8 m and height 3.5 m. Find its volume. How much cloth is required to just cover the heap?
A solid metal sphere is cut through its center into 2 equal parts. If the diameter of the sphere is `3 1/2 cm`, find the total surface area of each part correct to two decimal places.
The internal and external diameter of a hollow hemispherical vessel are 21 cm and 28 cm respectively. Find :
- internal curved surface area,
- external curved surface area,
- total surface area,
- volume of material of the vessel.
A hemispherical bowl of diameter 7.2 cm is filled completely with chocolate sauce. This sauce is poured into an inverted cone of radius 4.8 cm. Find the height of the cone if it is completely filled.
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find :
- the surface area of remaining solid,
- the volume of remaining solid,
- the weight of the material drilled out if it weighs 7 gm per cm3.
Surface area of a cone is 188.4 sq.cm and its slant height is 10 cm. Find its perpendicular height ( π= 3.14)
Total surface area of a cone is 616 sq.cm. If the slant height of the cone is three times the radius of its base, find its slant height.
A sphere and a cone have the same radii. If their volumes are also equal, prove that the height of the cone is twice its radius.
A hollow metallic cylindrical tube has an internal radius of 3.5 cm and height 21 cm. The thickness of the metal tube is 0.5 cm. The tube is melted and cast into a right circular cone of height 7 cm. Find the radius of the cone, correct to one decimal place.
A cone and a hemisphere have equal bases and equal volumes. Find the ratio of their heights.
The circumference of the base of a 10 m high conical tent is 44 metres. Calculate the length of canvas used in making the tent if the width of the canvas is 2m. (Take π = 22/7)
A cloth having an area of 165 m2 is shaped into the form of a conical tent of radius 5 m. How many students can sit in the tent if a student, on an average, occupies `5/7` m2 on the ground?
A cloth having an area of 165 m2 is shaped into the form of a conical tent of radius 5 m. Find the volume of the cone.
