Advertisements
Advertisements
प्रश्न
A cone and a hemisphere have equal bases and equal volumes. Find the ratio of their heights.
उत्तर
Let, the height of cone = h and height of hemisphere = H
∴ Volume of cone = Volume of hemisphere
`1/3 πr^2h = 2/3 πr^3`
`1/3 πr^2h = 2/3 πr^2"H` ...( ∵ H = r )
`h/H = (2πr^2 xx 3)/(3 πr^2)`
`h/H = 2/1`
h: H = 2: 1.
APPEARS IN
संबंधित प्रश्न
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
`["Assume "pi=22/7]`
A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is ₹ 12 per m2, what will be the cost of painting all these cones?
`("Use "π = 3.14" and take "sqrt1.04= 1.02)`
The radius of a cone is 5 cm and vertical height is 12 cm. Find the area of the curved surface.
The radius of a cone is 7 cm and area of curved surface is 176 `cm^2`. Find the slant height.
Find the total surface area of a right circular cone with radius 6 cm and height 8 cm.
A conical tent is 10 m high and the radius of its base is 24 m. Find the slant height of the tent. If the cost of 1 2 m canvas is Rs. 70, find the cost of the canvas required to make the tent.
Find the volume of a right circular cone with:
radius 3.5 cm, height 12 cm
The circumference of the base of a 12 m high conical tent is 66 m. Find the volume of the air contained in it.
The radius and the height of a right circular cone are in the ratio 5 : 12 and its volume is 2512 cubic cm. Find the radius and slant height of the cone. (Take π = 3.14)
A solid metal sphere is cut through its center into 2 equal parts. If the diameter of the sphere is `3 1/2 cm`, find the total surface area of each part correct to two decimal places.
A solid metallic cone, with radius 6 cm and height 10 cm, is made of some heavy metal A. In order to reduce its weight, a conical hole is made in the cone as shown and it is completely filled with a lighter metal B. The conical hole has a diameter of 6 cm and depth 4 cm. Calculate the ratio of the volume of metal A to the volume of the metal B in the solid.
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find :
- the surface area of remaining solid,
- the volume of remaining solid,
- the weight of the material drilled out if it weighs 7 gm per cm3.
A cubical block of side 7 cm is surmounted by a hemisphere of the largest size. Find the surface area of the resulting solid.
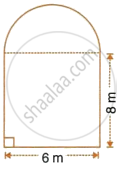
The cross-section of a railway tunnel is a rectangle 6 m broad and 8 m high surmounted by a semi-circle as shown in the figure. The tunnel is 35 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs. 2.25 per m2.
A solid, consisting of a right circular cone standing one a hemisphere, is placed upright in a right circular cylinder, full of water, and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm; the radius of
the hemisphere is 2 cm and the height of cone is 4 cm. Give your answer to the nearest cubic centimeter.
Find the volume of the right circular cone whose height is 12 cm and slant length is 15 cm . (π = 3.14)
A buoy is made in the form of a hemisphere surmounted by a right circular cone whose circular base coincides with the plane surface of the hemisphere. The radius of the base of the cone is 3.5 m and its volume is two-third the volume of hemisphere. Calculate the height of the cone and the surface area of the buoy, correct to two decimal places.
Find the cost of painting a hemispherical dome of diameter 10 m at the rate of Rs 1.40 per square metre.
The volume of a conical tent is 1232 m3 and the area of the base floor is 154 m2. Calculate the: length of the canvas required to cover this conical tent if its width is 2 m.
A vessel in the form of an inverted cone is filled with water to the brim: Its height is 20 cm and the diameter is 16.8 cm. Two equal solid cones are dropped in it so that they are fully submerged. As a result, one-third of the water in the original cone overflows. What is the volume of each of the solid cones submerged?
