Advertisements
Advertisements
प्रश्न
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find :
- the surface area of remaining solid,
- the volume of remaining solid,
- the weight of the material drilled out if it weighs 7 gm per cm3.
उत्तर
i. Total surface area of cuboid = 2(lb + bh + lh)
= 2(42 × 30 + 30 × 20 + 20 × 42)
= 2(1260 + 600 + 840)
= 2 × 2700
= 5400 cm2
Diameter of the cone = 14 cm
Radius of the cone = `14/2` = 7 cm
Area of circular base = πr2
= `22/7 xx 7 xx 7`
= 154 cm2
Area of curved surface area of cone = πrl
= `22/7 xx 7 xx sqrt(7^2 + 24^2)`
= `22sqrt(49 + 576)`
= 22 × 25
= 550 cm2
Surface area of remaining part = 5400 + 550 – 154 = 5796 cm2
ii. Dimensions of rectangular solids = (42 × 30 × 20) cm
Volume = (42 × 30 × 20) = 25200 cm3
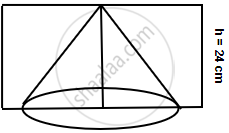
Radius of conical cavity (r) = 7 cm
Height (h) = 24 cm
Volume of cone = `1/3pir^2h`
= `1/3 xx 22/7 xx 7 xx 7 xx 24`
= 1232 cm3
Volume of remaining solid = (25200 – 1232) = 23968 cm3
iii. Weight of material drilled out
= 1232 × 7 g
= 8624 g
= 8.624 kg
APPEARS IN
संबंधित प्रश्न
Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
`["Assume "pi=22/7]`
The radius of a cone is 7 cm and area of curved surface is 176 `cm^2`. Find the slant height.
Find the ratio of the curved surface areas of two cones if their diameters of the bases are equal and slant heights are in the ratio 4 : 3.
Find the volume of a right circular cone with:
radius 3.5 cm, height 12 cm
Two cones have their heights in the ratio 1 : 3 and the radii of their bases in the ratio 3 : 1. Find the ratio of their volumes.
If the radius of the base of a cone is halved, keeping the height same, what is the ratio of the volume of the reduced cone to that of the original cone?
A heap of wheat is in the form of a cone of diameter 9 m and height 3.5 m. Find its volume. How much canvas cloth is required to just cover the heap? (Use 𝜋 = 3.14).
The diameter of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surface areas.
A solid cone of height 8 cm and base radius 6 cm is melted and recast into identical cones, each of height 2 cm and diameter 1 cm. Find the number of cones formed.
The internal and external diameter of a hollow hemispherical vessel are 21 cm and 28 cm respectively. Find :
- internal curved surface area,
- external curved surface area,
- total surface area,
- volume of material of the vessel.
The radii of the bases of two solid right circular cones of same height are r1 and r2 respectively. The cones are melted and recast into a solid sphere of radius R. Find the height of each cone in terms r1, r2 and R.
The curved surface area of a cone is 2200 sq.cm and its slant height is 50 cm. Find the total surface area of cone. `(π = 22/7)`
Find the cost of painting a hemispherical dome of diameter 10 m at the rate of Rs 1.40 per square metre.
A hollow metallic cylindrical tube has an internal radius of 3.5 cm and height 21 cm. The thickness of the metal tube is 0.5 cm. The tube is melted and cast into a right circular cone of height 7 cm. Find the radius of the cone, correct to one decimal place.
The volume of a conical tent is 1232 m3 and the area of the base floor is 154 m2. Calculate the: height of the tent.
The internal and external diameters of a hollow hemi-spherical vessel are 21 cm and 28 cm respectively. Find: total surface area.
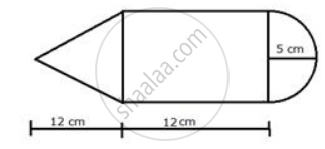
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown. Calculate: the total volume of the solid.
The radius and height of cone are in the ratio 3 : 4. If its volume is 301.44 cm3. What is its radius? What is its slant height? (Take π = 3.14)
Water flows at the rate of 10 m per minute through a cylindrical pipe 5 mm of diameter. How much time would it take to fill a conical vessel whose diameter at he surface is 40 cm and depth is 24 cm?
The curved surface area of a right circular cone of height 15 cm and base diameter 16 cm is
