Advertisements
Advertisements
Question
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find :
- the surface area of remaining solid,
- the volume of remaining solid,
- the weight of the material drilled out if it weighs 7 gm per cm3.
Solution
i. Total surface area of cuboid = 2(lb + bh + lh)
= 2(42 × 30 + 30 × 20 + 20 × 42)
= 2(1260 + 600 + 840)
= 2 × 2700
= 5400 cm2
Diameter of the cone = 14 cm
Radius of the cone = `14/2` = 7 cm
Area of circular base = πr2
= `22/7 xx 7 xx 7`
= 154 cm2
Area of curved surface area of cone = πrl
= `22/7 xx 7 xx sqrt(7^2 + 24^2)`
= `22sqrt(49 + 576)`
= 22 × 25
= 550 cm2
Surface area of remaining part = 5400 + 550 – 154 = 5796 cm2
ii. Dimensions of rectangular solids = (42 × 30 × 20) cm
Volume = (42 × 30 × 20) = 25200 cm3
Radius of conical cavity (r) = 7 cm
Height (h) = 24 cm
Volume of cone = `1/3pir^2h`
= `1/3 xx 22/7 xx 7 xx 7 xx 24`
= 1232 cm3
Volume of remaining solid = (25200 – 1232) = 23968 cm3
iii. Weight of material drilled out
= 1232 × 7 g
= 8624 g
= 8.624 kg
APPEARS IN
RELATED QUESTIONS
A joker’s cap is in the form of right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
`["Assume "pi=22/7]`
The radius of a cone is 5 cm and vertical height is 12 cm. Find the area of the curved surface.
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
There are two cones. The curved surface area of one is twice that of the other. The slant height of the later is twice that of the former. Find the ratio of their radii.
The radius and the height of a right circular cone are in the ratio 5 : 12. If its volume is 314 cubic meter, find the slant height and the radius (Use it 𝜋 = 3.14).
A cylinder and a cone have equal radii of their bases and equal heights. Show that their volumes are in the ratio 3:1.
If the radius of the base of a cone is halved, keeping the height same, what is the ratio of the volume of the reduced cone to that of the original cone?
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilo litres?
Find the volume of a cone whose slant height is 17 cm and radius of base is 8 cm.
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm, are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
The radii of the bases of two solid right circular cones of same height are r1 and r2 respectively. The cones are melted and recast into a solid sphere of radius R. Find the height of each cone in terms r1, r2 and R.
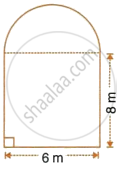
The cross-section of a railway tunnel is a rectangle 6 m broad and 8 m high surmounted by a semi-circle as shown in the figure. The tunnel is 35 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs. 2.25 per m2.
Total surface area of a cone is 616 sq.cm. If the slant height of the cone is three times the radius of its base, find its slant height.
The curved surface area of a right circular cone of radius 11.3 cm is 710 cm2. What is the slant height of the cone ?
The radius and height of a cylinder, a cone and a sphere are same. Calculate the ratio of their volumes.
The total surface area of a right circular cone of slant height 13 cm is 90π cm2. Calculate: its volume in cm3. Take π = 3.14
A cone and a hemisphere have equal bases and equal volumes. Find the ratio of their heights.
The circumference of the base of a 10 m high conical tent is 44 metres. Calculate the length of canvas used in making the tent if the width of the canvas is 2m. (Take π = 22/7)
The ratio of the radii of two right circular cones of the same height is 1 : 3. Find the ratio of their curved surface area when the height cone is 3 times the radius of the smaller cone.
A cloth having an area of 165 m2 is shaped into the form of a conical tent of radius 5 m. Find the volume of the cone.
