Advertisements
Advertisements
Question
The ratio of the radii of two right circular cones of the same height is 1 : 3. Find the ratio of their curved surface area when the height cone is 3 times the radius of the smaller cone.
Solution
Let the radius of the first cone be ‘x’ and the Height of the cone be 3x
l = `sqrt("h"^2 + "r"^2)`
= `sqrt((3x)^2 + x^2)`
= `sqrt(10x^2)`
C.S.A. of the first cone = πrl sq.units
= `pi xx x sqrt(10x^2)`
= `pi x^2 sqrt(10)`
The radius and the height of the second cone is 3x ...(Given)
l = `sqrt((3x)^2 + (3x)^2)`
= `sqrt(9x^2 + 9x^2)`
= `sqrt(18x^2)`
C.S.A of the second one
= `pi xx 3x xx sqrt(18x^2)`
= `pi xx 3x^2 xx sqrt(9 xx 2)`
= `pi 9x^2 sqrt(2)`
Ratio of the curves surface area
= `pix^2 sqrt(10) : 9 pi x^2 sqrt(2)`
= `sqrt(10) : 9sqrt(2)`
= `sqrt(2) xx sqrt(5) : 9sqrt(2)`
= `sqrt(5) : 9`
APPEARS IN
RELATED QUESTIONS
A conical tent is 10 m high and the radius of its base is 24 m. Find
- slant height of the tent.
- cost of the canvas required to make the tent, if the cost of 1 m2 canvas is ₹ 70.
`["Assume "pi=22/7]`
The radius of a cone is 5 cm and vertical height is 12 cm. Find the area of the curved surface.
Find the total surface area of a right circular cone with radius 6 cm and height 8 cm.
What length of tarpaulin 3 m wide will be required to make a conical tent of height 8 m and base radius 6 m? Assume that the extra length of material will be required for stitching margins and wastage in cutting is approximately 20 cm (Use it 𝜋 = 3.14)
The ratio of volumes of two cones is 4 : 5 and the ratio of the radii of their bases is 2:3. Find the ratio of their vertical heights.
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilo litres?
The curved surface area of a cone is 12320 cm2. If the radius of its base is 56 cm, find its height.
A hollow metallic cylindrical tube has an internal radius of 3.5 cm and height 21 cm. The thickness of the metal tube is 0.5 cm. The tube is melted and cast into a right circular cone of height 7 cm. Find the radius of the cone, correct to one decimal place.
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown. Calculate: the total volume of the solid.
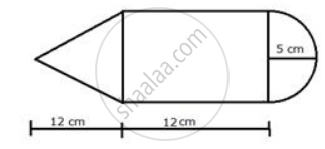
A cone and a hemisphere have equal bases and equal volumes. Find the ratio of their heights.
