Advertisements
Advertisements
Question
A conical tent is 10 m high and the radius of its base is 24 m. Find
- slant height of the tent.
- cost of the canvas required to make the tent, if the cost of 1 m2 canvas is ₹ 70.
`["Assume "pi=22/7]`
Solution
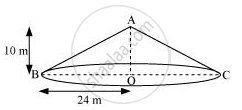
(i) Let ABC be a conical tent.
Height (h) of conical tent = 10 m
Radius (r) of conical tent = 24 m
Let the slant height of the tent be l.
In ΔABO,
AB2 = AO2 + BO2
l2 = h2 + r2
= (10 m)2 + (24 m)2
= 676 m2
∴ l = 26 m
Therefore, the slant height of the tent is 26 m.
(ii) Curved surface area of the tent = πrl
= `(22/7xx24xx26)m^2`
= `13728/7 m^2`
Cost of 1 m2 canvas = ₹ 70
`"Cost of "13728/7 m^2 " canvas"` = `₹ (13728/7xx70)`
= ₹ 137280
Therefore, the cost of the canvas required to make such a tent is ₹ 137280.
APPEARS IN
RELATED QUESTIONS
The curved surface area of a cone is 4070 cm2 and its diameter is 70 cm. What is its slant height? (Use it 𝜋 = 22/7).
A conical tent is 10 m high and the radius of its base is 24 m. Find the slant height of the tent. If the cost of 1 2 m canvas is Rs. 70, find the cost of the canvas required to make the tent.
The radius and height of a right circular cone are in the ratio 5 : 12 and its volume is 2512 cubic cm. Find the slant height and radius of the cone. (Use it 𝜋 = 3.14).
The volume of a right circular cone is 9856 cm3. If the diameter of the base is 28 cm, find:
(i) height of the cone (ii) slant height of the cone (iii) curved surface area of the cone.
The circumference of the base of a 12 m high conical tent is 66 m. Find the volume of the air contained in it.
A solid cone of height 8 cm and base radius 6 cm is melted and recast into identical cones, each of height 2 cm and diameter 1 cm. Find the number of cones formed.
The total surface area of a right circular cone of slant height 13 cm is 90π cm2.
Calculate:
- its radius in cm.
- its volume in cm3. [Take π = 3.14].
The ratio of the base area and the curved surface of a conical tent is 40: 41. If the height is 18 m, Find the air capacity of the tent in terms of n.
A vessel in the form of an inverted cone is filled with water to the brim: Its height is 20 cm and the diameter is 16.8 cm. Two equal solid cones are dropped in it so that they are fully submerged. As a result, one-third of the water in the original cone overflows. What is the volume of each of the solid cones submerged?
A right-angled triangle PQR where ∠Q = 90° is rotated about QR and PQ. If QR = 16 cm and PR = 20 cm, compare the curved surface areas of the right circular cones so formed by the triangle
