Advertisements
Advertisements
Question
A right-angled triangle PQR where ∠Q = 90° is rotated about QR and PQ. If QR = 16 cm and PR = 20 cm, compare the curved surface areas of the right circular cones so formed by the triangle
Solution
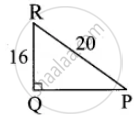
In the Right Triangle
QP2 = PR2 – QR2
= 202 – 162
= 400 – 256
= 144
QP = `sqrt(144)` = 12 cm
When PQ is rotated r = 12, l = 20
C.S.A of the cone = πrl sq. units
= π × 12 × 20 cm2
= 240π cm2
When QR is rotated r = 16, l = 20
C.S.A of the cone = nrl sq. units
= π × 16 × 20
= 320π cm2
C.S.A. of a cone when rotated about QR is larger.
APPEARS IN
RELATED QUESTIONS
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of ₹ 210 per 100 m2.
`["Assume "pi=22/7]`
Curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find the radius of the base and total surface area of the cone.
Find the volume of a right circular cone with:
height 21 cm and slant height 28 cm.
A cylinder and a cone have equal radii of their bases and equal heights. Show that their volumes are in the ratio 3:1.
A solid metal sphere is cut through its center into 2 equal parts. If the diameter of the sphere is `3 1/2 cm`, find the total surface area of each part correct to two decimal places.
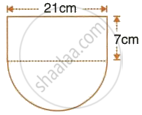
The given figure shows the cross section of a water channel consisting of a rectangle and a semi-circle. Assuming that the channel is always full, find the volume of water discharged through it in one minute if water is flowing at the rate of 20 cm per second. Give your answer in cubic metres correct to one place of decimal.
The radius and height of a cylinder, a cone and a sphere are same. Calculate the ratio of their volumes.
A buoy is made in the form of a hemisphere surmounted by a right circular cone whose circular base coincides with the plane surface of the hemisphere. The radius of the base of the cone is 3.5 m and its volume is two-third the volume of hemisphere. Calculate the height of the cone and the surface area of the buoy, correct to two decimal places.
The total surface area of a right circular cone of slant height 13 cm is 90π cm2. Calculate: its volume in cm3. Take π = 3.14
A conical tent is accommodate to 11 persons each person must have 4 sq. metre of the space on the ground and 20 cubic metre of air to breath. Find the height of the cone.
