Advertisements
Advertisements
प्रश्न
A right-angled triangle PQR where ∠Q = 90° is rotated about QR and PQ. If QR = 16 cm and PR = 20 cm, compare the curved surface areas of the right circular cones so formed by the triangle
उत्तर
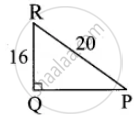
In the Right Triangle
QP2 = PR2 – QR2
= 202 – 162
= 400 – 256
= 144
QP = `sqrt(144)` = 12 cm
When PQ is rotated r = 12, l = 20
C.S.A of the cone = πrl sq. units
= π × 12 × 20 cm2
= 240π cm2
When QR is rotated r = 16, l = 20
C.S.A of the cone = nrl sq. units
= π × 16 × 20
= 320π cm2
C.S.A. of a cone when rotated about QR is larger.
APPEARS IN
संबंधित प्रश्न
The area of the curved surface of a cone is 60 cm2. If the slant height of the cone be 8 cm, find the radius of the base?
Find the ratio of the curved surface areas of two cones if their diameters of the bases are equal and slant heights are in the ratio 4 : 3.
The circumference of the base of a 10 m height conical tent is 44 metres. Calculate the length of canvas used in making the tent if width of canvas is 2 m. (Use it 𝜋= 22/7).
Find the volume of a right circular cone with:
height 21 cm and slant height 28 cm.
A solid cone of height 8 cm and base radius 6 cm is melted and recast into identical cones, each of height 2 cm and diameter 1 cm. Find the number of cones formed.
The area of the base of a conical solid is 38.5 cm2 and its volume is 154 cm3. Find the curved surface area of the solid.
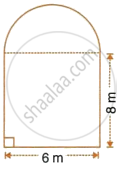
The cross-section of a railway tunnel is a rectangle 6 m broad and 8 m high surmounted by a semi-circle as shown in the figure. The tunnel is 35 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs. 2.25 per m2.
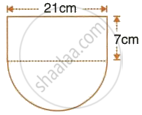
The given figure shows the cross section of a water channel consisting of a rectangle and a semi-circle. Assuming that the channel is always full, find the volume of water discharged through it in one minute if water is flowing at the rate of 20 cm per second. Give your answer in cubic metres correct to one place of decimal.
The heights of two cones are in the ratio 1:3 and their base radii are in the ratio 3:1. Find the ratio of their volumes.
The ratio of the radii of two right circular cones of the same height is 1 : 3. Find the ratio of their curved surface area when the height cone is 3 times the radius of the smaller cone.
