Advertisements
Advertisements
Question
The curved surface area of a cone is 4070 cm2 and its diameter is 70 cm. What is its slant height? (Use it 𝜋 = 22/7).
Solution
Given diameter= 70 cm
⇒ 2r = 70 cm
⇒ r=35cm
Now, curved surface area = `4070cm^2`
⇒ `pirl=4070`
Where r=radius of the cone
l=slant height of the cone
∴ `pirl=4070`
⇒ `22/7xx35xxl=4070`
⇒`l=(4070xx7)/(22xx35)=37cm`
∴ Slant height of the cone= 37 cm
APPEARS IN
RELATED QUESTIONS
The following figure represents a solid consisting of a right circular cylinder with a hemisphere at one end and a cone at the other. This common radius is 7 cm. The height of the cylinder and cone are each of 4 cm. Find the volume of the solid.

The radius and slant height of a cone are In the ratio of 4 : 7. If its curved surface area is 792 cm2, find its radius. (Use it 𝜋 = 22/7).
A right angled triangle of which the sides containing he right angle are 6.3 cm and lo cm in length, is made to turn round on the longer side. Find the volume of the solid, thus generated. Also, find its curved surface area.
Find the volume of the largest right circular cone that can be fitted in a cube whose edge is 14 cm.
The circumference of the base of a 12 m high conical tent is 66 m. Find the volume of the air contained in it.
There are two cones. The curved surface area of one is twice that of the other. The slant height of the latter is twice that of the former. Find the ratio of their radii.
A hemispherical bowl of diameter 7.2 cm is filled completely with chocolate sauce. This sauce is poured into an inverted cone of radius 4.8 cm. Find the height of the cone if it is completely filled.
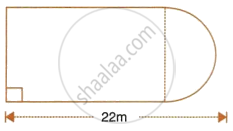
In the following diagram a rectangular platform with a semi-circular end on one side is 22 metres long from one end to the other end. If the length of the half circumference is 11 metres, find the cost of constructing the platform, 1.5 metres high at the rate of Rs. 4 per cubic metres.
Volume of a cone is 1232 cm3 and its height is 24 cm. Find the surface area of the cone. `( π = 22/7)`
A vessel in the form of an inverted cone is filled with water to the brim: Its height is 20 cm and the diameter is 16.8 cm. Two equal solid cones are dropped in it so that they are fully submerged. As a result, one-third of the water in the original cone overflows. What is the volume of each of the solid cones submerged?
