Advertisements
Advertisements
Question
There are two cones. The curved surface area of one is twice that of the other. The slant height of the latter is twice that of the former. Find the ratio of their radii.
Solution
Let slant height of the first cone = l
Then slant height of the second cone = 2l
Radius of the first cone = r1
Radius of the second cone = r2
Then, curved surface area of first cone = πr1l
Curved surface area of second cone = πr2(2l) = 2πr2l
According to given condition:
πr1l = 2(2πr2l)
π πr1l = 4πr2l
r1 = 4r2
`r_1/r_2 = 4/1`
∴ r1 : r2 = 4 : 1
APPEARS IN
RELATED QUESTIONS
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
`["Assume "pi=22/7]`
A joker’s cap is in the form of right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
`["Assume "pi=22/7]`
The following figure represents a solid consisting of a right circular cylinder with a hemisphere at one end and a cone at the other. This common radius is 7 cm. The height of the cylinder and cone are each of 4 cm. Find the volume of the solid.

Find the curved surface area of a cone, if its slant height is 60 cm and the radius of its base is 21 cm.
A Joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
The diameters of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surfaces.
A cylinder and a cone have equal radii of their bases and equal heights. Show that their volumes are in the ratio 3:1.
The curved surface area of a cone is 12320 cm2. If the radius of its base is 56 cm, find its height.
Two right circular cone x and y are made x having three times the radius of y and y having half the volume of x. Calculate the ratio between the heights of x and y.
A solid metal sphere is cut through its center into 2 equal parts. If the diameter of the sphere is `3 1/2 cm`, find the total surface area of each part correct to two decimal places.
A solid metallic hemisphere of diameter 28 cm is melted and recast into a number of identical solid cones, each of diameter 14 cm and height 8 cm. Find the number of cones so formed.
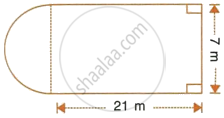
The horizontal cross-section of a water tank is in the shape of a rectangle with semi-circle at one end, as shown in the following figure. The water is 2.4 metres deep in the tank. Calculate the volume of water in the tank in gallons.
A solid, consisting of a right circular cone standing one a hemisphere, is placed upright in a right circular cylinder, full of water, and touches the bottom. Find the volume of water left in the cylinder, having given that the radius of the cylinder is 3 cm and its height is 6 cm; the radius of
the hemisphere is 2 cm and the height of cone is 4 cm. Give your answer to the nearest cubic centimeter.
A solid is in the form of a right circular cone mounted on a hemisphere. The diameter of the base of the cone, which exactly coincides with hemisphere, is 7 cm and its height is 8 cm. The solid is placed in a cylindrical vessel of internal radius 7 cm and height 10 cm. How much water, in cm3, will be required to fill the vessel completely?
What will be the cost of making a closed cone of tin sheet having radius of base 6 m and slant height 8 m if the rate of making is Rs.10 per sq.m? `(π = 22/7)`
Find the curved surface area of a cone whose height is 8 cm and base diameter is 12 cm .
Find the cost of painting a hemispherical dome of diameter 10 m at the rate of Rs 1.40 per square metre.
The surface area of a solid sphere is increased by 21% without changing its shape. Find the percentage increase in its: volume
The circumference of the base of a 10 m high conical tent is 44 metres. Calculate the length of canvas used in making the tent if the width of the canvas is 2m. (Take π = 22/7)
