Advertisements
Advertisements
Question
If the radius of the base of a cone is halved, keeping the height same, what is the ratio of the volume of the reduced cone to that of the original cone?
Solution
Let radius of cone is r and height is h
Volume `V1=1/3pir^2h `
In another case,
Radius of cone = half of radius =` r/2`
Height =h
∴ `Volume= (V_2)=1/3pi(1/2r)^2h`
=` 1/3pixxr^2/4xxh`
= `1/12pir^2h`
∴ `V_1/V_2=(1/12pir^2h)/(1/3pir^2h)=3/12=1/4`
∴ Ratio will be (1:4).
APPEARS IN
RELATED QUESTIONS
A hemispherical bowl of diameter 7.2 cm is filled completely with chocolate sauce. This sauce is poured into an inverted cone of radius 4.8 cm. Find the height of the cone.
The height of a cone is 21 cm. Find the area of the base if the slant height is 28 cm.
Find the volume of a right circular cone with:
radius 6 cm, height 7 cm.
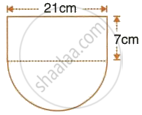
The given figure shows the cross section of a water channel consisting of a rectangle and a semi-circle. Assuming that the channel is always full, find the volume of water discharged through it in one minute if water is flowing at the rate of 20 cm per second. Give your answer in cubic metres correct to one place of decimal.
What will be the cost of making a closed cone of tin sheet having radius of base 6 m and slant height 8 m if the rate of making is Rs.10 per sq.m? `(π = 22/7)`
Surface area of a cone is 188.4 sq.cm and its slant height is 10 cm. Find its perpendicular height ( π= 3.14)
The radius and height of a cylinder, a cone and a sphere are same. Calculate the ratio of their volumes.
A sphere and a cone have the same radii. If their volumes are also equal, prove that the height of the cone is twice its radius.
The internal and external diameters of a hollow hemi-spherical vessel are 21 cm and 28 cm respectively. Find: external curved surface area .
The internal and external diameters of a hollow hemi-spherical vessel are 21 cm and 28 cm respectively. Find: total surface area.
