Advertisements
Advertisements
प्रश्न
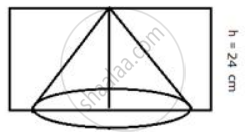
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find: the volume of remaining solid
उत्तर
Dimensions of rectangular solids = `=(42xx30xx20) "cm"`
volume=`(42xx30xx20)=25200 "cm"^3 `
Radius of conical cavity (r) =7 cm
height (h)=24 cm
Volume of cone=`1/3pir^2h`
=`1/3xx22/7xx7xx7xx24`
`= 1232 "cm"^3`
Volume of remaining solid =` (25200-1232)=23968 "cm"^3`
Radius of conical cavity (r) =7 cm
height (h) = 24 cm
Volume of cone = `1/3 pi "r"^2"h"`
`= 1/3 xx 22/7 xx 7 xx 7 xx 24`
= 1232 cm3
Volume of remaining solid = (25200 - 1232) = 23968 cm3
APPEARS IN
संबंधित प्रश्न
On a map drawn to a scale of 1: 50,000, a rectangular plot of land ABCD has the following dimensions. AB = 6 cm; BC = 8 cm and all angles are right angles. Find:
1) the actual length of the diagonal distance AC of the plot in km.
2) the actual area of the plot in sq. km.
Find the surface area of a sphere of radius 5.6 cm .
Find the surface area of a sphere of diameter 14 cm .
Find the surface area of a sphere of diameter 21 cm .
Find the surface area of a sphere of diameter 3.5 cm .
The surface area of a sphere is 5544 `cm^2`, find its diameter.
The volume of a sphere is 38808 cm3; find its diameter and the surface area.
A solid rectangular block of metal 49 cm by 44 cm by 18 cm is melted and formed into a solid sphere. Calculate the radius of the sphere.
Spherical marbles of diameter 1.4 cm are dropped into beaker containing some water and are fully submerged. The diameter of the beaker is 7 cm. Find how many marbles have been dropped in it if the water rises by 5.6 cm.
Find the radius of a sphere whose surface area is 154 cm2.
A sphere is placed inside a right circular cylinder so as to touch the top, base and lateral surface of the cylinder. If the radius of the sphere is r, then the volume of the cylinder is
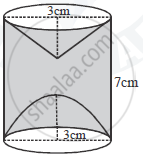
A hemispherical and a conical hole is scooped out of a.solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows:
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm.
Give your answer correct to the nearest whole number.Taken`pi = 22/7`.
The model of a building is constructed with the scale factor 1 : 30.
(i) If the height of the model is 80 cm, find the actual height of the building in meters.
(ii) If the actual volume of a tank at the top of the building is 27m3, find the volume of the tank on the top of the model.
Find the volume of a sphere, if its surface area is 154 sq.cm.
Find the length of the wire of diameter 4 m that can be drawn from a solid sphere of radius 9 m.
A solid metallic cylinder has a radius of 2 cm and is 45 cm tall. Find the number of metallic spheres of diameter 6 cm that can be made by recasting this cylinder .
Find the volume of the hollow sphere whose inner diameter is 8 cm and the thickness of the material of which it is made is 1 cm .
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown.
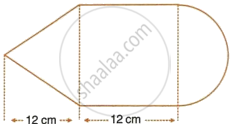
Calculate :
- the total surface area.
- the total volume of the solid and
- the density of the material if its total weight is 1.7 kg.
Find the volume and surface area of a sphere of diameter 21 cm.
The radius of a sphere is 10 cm. If we increase the radius 5% then how many % will increase in volume?
