Advertisements
Advertisements
प्रश्न
The surface area of a sphere is 5544 `cm^2`, find its diameter.
उत्तर
Surface area of a sphere is 5544cm^2`
⇒`4πr^2 - 5544`
⇒`(4×22)/7 × r^2 -5544`
⇒`r^2 - (5544 × 7)/88`
⇒ r - `sqrt(21 cm × 21 cm) - sqrt ((21)^2 cm) `
⇒ r - 21 cm
Diameter = 2 (radius )
-2 (21cm)
- 42 cm .
APPEARS IN
संबंधित प्रश्न
Find the total surface area of a hemisphere of radius 10 cm. [Use π = 3.14]
A right circular cylinder just encloses a sphere of radius r (see figure). Find
- surface area of the sphere,
- curved surface area of the cylinder,
- ratio of the areas obtained in (i) and (ii).

Metallic spheres of radii 6 cm, 8 cm and 10 cm respectively are melted and recasted into a single solid sphere. Taking π = 3.1, find the surface area of the solid sphere formed.
A hollow sphere of internal and external diameter 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone.
A cylindrical rod whose height is 8 times of its radius is melted and recast into spherical balls of same radius. The number of balls will be
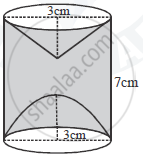
A hemispherical and a conical hole is scooped out of a.solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows:
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm.
Give your answer correct to the nearest whole number.Taken`pi = 22/7`.
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find: the weight of the material drilled out if it weighs 7 gm per cm3.
A sphere cut out from a side of 7 cm cubes. Find the volume of this sphere?
How many spherical bullets can be made out of a solid cube of lead whose edge measures 44 cm, each bullet being 4 cm in diameter?
A solid sphere is cut into two identical hemispheres.
Statement 1: The total volume of two hemispheres is equal to the volume of the original sphere.
Statement 2: The total surface area of two hemispheres together is equal to the surface area of the original sphere.
Which of the following is valid?
