Advertisements
Advertisements
प्रश्न
The model of a building is constructed with the scale factor 1 : 30.
(i) If the height of the model is 80 cm, find the actual height of the building in meters.
(ii) If the actual volume of a tank at the top of the building is 27m3, find the volume of the tank on the top of the model.
उत्तर
(i) If the scale factor is 1 : 30°, then actual height will be 30 times the height of the model.
∴ Actual height = 80cm × 30cm
= 2400cm
Actual height = 24 m
(ii) Now, actual volume of a tank will be (30)3 times the volume of a tank in the model.
∴ Volume of tank in model × (30)3 = Actual volume of a tank
Volume of tank in the model = `((27))/((30)^3 ) "m"^3`
`= (27 xx 10^6) /(30 xx 30xx 30 ) " cm"^3`
` = 1000" cm"^3`
APPEARS IN
संबंधित प्रश्न
Find the surface area of a sphere of diameter 3.5 m.
`["Assume "pi=22/7]`
The diameter of the moon is approximately one-fourth of the diameter of the earth. Find the ratio of their surface area.
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate:
- the radius of the sphere.
- the number of cones recast. (Take π = `22/7`)
The dome of a building is in the form of a hemisphere. Its radius is 63 dm. Find the cost of
painting it at the rate of Rs. 2 per sq. m.
The volume of one sphere is 27 times that of another sphere. Calculate the ratio of their :
- radii,
- surface areas.
If the number of square centimeters on the surface of a sphere is equal to the number of cubic centimeters in its volume, what is the diameter of the sphere?
A solid rectangular block of metal 49 cm by 44 cm by 18 cm is melted and formed into a solid sphere. Calculate the radius of the sphere.
A hollow sphere of internal and external radii 6 cm and 8 cm respectively is melted and recast into small cones of base radius 2 cm and height 8 cm. Find the number of cones.
A solid is in the form of a cone standing on a hemi-sphere with both their radii being equal to 8 cm and the height of cone is equal to its radius. Find, in terms of π, the volume of the solid.
The hollow sphere, in which the circus motor cyclist performs his stunts, has a diameter of 7 m. Find the area available to the motorcyclist for riding.
If a sphere is inscribed in a cube, then the ratio of the volume of the sphere to the volume of the cube is
A hemispherical bowl of internal radius 9 cm is full of liquid. This liquid is to be filled into conical shaped small containers each of diameter 3 cm and height 4 cm. How many containers are necessary to empty the bowl?
The total area of a solid metallic sphere is 1256 cm2. It is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate: the number of cones recasted [π = 3.14]
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate : the number of cones recast. `("Take" pi =22/7)`
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown.
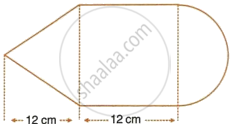
Calculate :
- the total surface area.
- the total volume of the solid and
- the density of the material if its total weight is 1.7 kg.
The volume of a sphere is 905 1/7 cm3, find its diameter.
A spherical ball of radius 3 cm is melted and recast into three spherical balls. The radii of two of the balls are 1.5 cm and 2 cm. Find the diameter of the third ball.
The radius of a hemispherical balloon increases from 6 cm to 12 cm as air is being pumped into it. The ratios of the surface areas of the balloon in the two cases is ______.
A solid sphere is cut into two identical hemispheres.
Statement 1: The total volume of two hemispheres is equal to the volume of the original sphere.
Statement 2: The total surface area of two hemispheres together is equal to the surface area of the original sphere.
Which of the following is valid?
