Advertisements
Advertisements
प्रश्न
A solid is in the form of a cone standing on a hemi-sphere with both their radii being equal to 8 cm and the height of cone is equal to its radius. Find, in terms of π, the volume of the solid.
उत्तर
Given, Radius of each cone and hemi-sphere (r) = 8 cm
Height of cone (h) = r = 8 cm
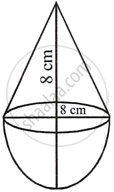
∴ Volume of solid
= `1/3pir^2h + 2/3pir^3`
= `1/3pir^2(h + 2r) cm^3`
= `1/3pi xx 8 xx 8(8 + 2 xx 8) cm^3`
= `64/3 pi(8 + 16) cm^3`
= `64/3pi xx 24`
= 512 π cm3
APPEARS IN
संबंधित प्रश्न
Find the total surface area of a hemisphere of radius 10 cm. [Use π = 3.14]
A hollow sphere of internal and external radii 6 cm and 8 cm respectively is melted and recast into small cones of base radius 2 cm and height 8 cm. Find the number of cones.
Find the surface area of a sphere of radius 5.6 cm .
A wooden toy is in the form of a cone surmounted on a hemisphere. The diameter of the base
of the cone is 16 cm and its height is 15 cm. Find the cost of painting the toy at Rs. 7 per 100
`cm^2`.
A spherical ball of lead has been melted and made into identical smaller balls with radius equal to half the radius of the original one. How many such balls can be made?
How many balls each of radius 1 cm can be made by melting a bigger ball whose diameter is 8 cm?
Metallic spheres of radii 6 cm, 8 cm and 10 cm respectively are melted and recasted into a single solid sphere. Taking π = 3.1, find the surface area of the solid sphere formed.
Total volume of three identical cones is the same as that of a bigger cone whose height is 9 cm and diameter 40 cm. Find the radius of the base of each smaller cone, if height of each is 108 cm.
A solid rectangular block of metal 49 cm by 44 cm by 18 cm is melted and formed into a solid sphere. Calculate the radius of the sphere.
Spherical marbles of diameter 1.4 cm are dropped into beaker containing some water and are fully submerged. The diameter of the beaker is 7 cm. Find how many marbles have been dropped in it if the water rises by 5.6 cm.
The cross-section of a tunnel is a square of side 7 m surmounted by a semi-circle as shown in the adjoining figure. The tunnel is 80 m long.
Calculate:
- its volume,
- the surface area of the tunnel (excluding the floor) and
- its floor area.

Find the total surface area of a hemisphere of radius 10 cm.
Find the radius of a sphere whose surface area is 154 cm2.
If the ratio of volumes of two spheres is 1 : 8, then the ratio of their surface areas is
The model of a building is constructed with the scale factor 1 : 30.
(i) If the height of the model is 80 cm, find the actual height of the building in meters.
(ii) If the actual volume of a tank at the top of the building is 27m3, find the volume of the tank on the top of the model.
Find the volume of a sphere, if its surface area is 154 sq.cm.
A certain number of metallic cones, each of radius 2 cm and height 3 cm are melted and recast into a solid sphere of radius 6 cm. Find the number of cones used.
The radius of a sphere is 10 cm. If we increase the radius 5% then how many % will increase in volume?
A spherical ball of radius 3 cm is melted and recast into three spherical balls. The radii of two of the balls are 1.5 cm and 2 cm. Find the diameter of the third ball.
The radius of a sphere increases by 25%. Find the percentage increase in its surface area
