Advertisements
Advertisements
प्रश्न
Spherical marbles of diameter 1.4 cm are dropped into beaker containing some water and are fully submerged. The diameter of the beaker is 7 cm. Find how many marbles have been dropped in it if the water rises by 5.6 cm.
उत्तर
Given, diameter of spherical marble = 1.4 cm
∴ Radius = `1.4/2` = 0.7 cm.
Volume of one ball = `4/3pir^3`
= `4/3pi (0.7)^3 cm^3` ...(i)
Diameter of beaker = 7 cm
∴ Radius = `7/2` cm,
Height of water (h) = 5.6 cm
∴ Volume of water = πr2h
= `pi (7/2 xx 7/2 xx 5.6) cm^3`
∴ Required No of balls dropped
= `(pi xx 49 xx 56 xx 3)/(4 xx 10 xx 4pi xx (0.7)^3)`
= `(49 xx 56 xx 3 xx 10 xx 10 xx 10)/(4 xx 10 xx 7 xx 7 xx 7 xx 4)`
= 150
APPEARS IN
संबंधित प्रश्न
Find the surface area of a sphere of radius 5.6 cm .
Find the surface area of a sphere of diameter 14 cm .
A cylinder of same height and radius is placed on the top of a hemisphere. Find the curved
surface area of the shape if the length of the shape be 7 cm.
Eight metallic spheres; each of radius 2 mm, are melted and cast into a single sphere. Calculate the radius of the new sphere.
Find the total surface area of a hemisphere of radius 10 cm.
If a sphere of radius 2r has the same volume as that of a cone with circular base of radius r, then find the height of the cone.
The surface area of a sphere of radius 5 cm is five times the area of the curved surface of a cone of radius 4 cm. Find the height of the cone.
If a sphere is inscribed in a cube, find the ratio of the volume of cube to the volume of the sphere.
If a solid sphere of radius r is melted and cast into the shape of a solid cone of height r, then the radius of the base of the cone is
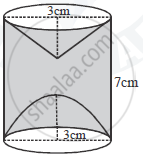
A hemispherical and a conical hole is scooped out of a.solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows:
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm.
Give your answer correct to the nearest whole number.Taken`pi = 22/7`.
The model of a building is constructed with the scale factor 1 : 30.
(i) If the height of the model is 80 cm, find the actual height of the building in meters.
(ii) If the actual volume of a tank at the top of the building is 27m3, find the volume of the tank on the top of the model.
Find the surface area of a sphere, if its volume is 38808 cubic cm. `(π = 22/7)`
Find the volume of a sphere, if its surface area is 154 sq.cm.
The internal and external diameters of a hollow hemi-spherical vessel are 21 cm and 28 cm respectively. Find volume of material of the vessel.
A certain number of metallic cones, each of radius 2 cm and height 3 cm are melted and recast into a solid sphere of radius 6 cm. Find the number of cones used.
A sphere cut out from a side of 7 cm cubes. Find the volume of this sphere?
The surface area of a solid metallic sphere is 616 cm2. It is melted and recast into smaller spheres of diameter 3.5 cm. How many such spheres can be obtained?
A solid sphere is cut into two identical hemispheres.
Statement 1: The total volume of two hemispheres is equal to the volume of the original sphere.
Statement 2: The total surface area of two hemispheres together is equal to the surface area of the original sphere.
Which of the following is valid?
A manufacturing company prepares spherical ball bearings, each of radius 7 mm and mass 4 gm. These ball bearings are packed into boxes. Each box can have maximum of 2156 cm3 of ball bearings. Find the:
- maximum number of ball bearings that each box can have.
- mass of each box of ball bearings in kg.
(use π = `22/7`)
