Advertisements
Advertisements
प्रश्न
Spherical marbles of diameter 1.4 cm are dropped into beaker containing some water and are fully submerged. The diameter of the beaker is 7 cm. Find how many marbles have been dropped in it if the water rises by 5.6 cm.
उत्तर
Given, diameter of spherical marble = 1.4 cm
∴ Radius = `1.4/2` = 0.7 cm.
Volume of one ball = `4/3pir^3`
= `4/3pi (0.7)^3 cm^3` ...(i)
Diameter of beaker = 7 cm
∴ Radius = `7/2` cm,
Height of water (h) = 5.6 cm
∴ Volume of water = πr2h
= `pi (7/2 xx 7/2 xx 5.6) cm^3`
∴ Required No of balls dropped
= `(pi xx 49 xx 56 xx 3)/(4 xx 10 xx 4pi xx (0.7)^3)`
= `(49 xx 56 xx 3 xx 10 xx 10 xx 10)/(4 xx 10 xx 7 xx 7 xx 7 xx 4)`
= 150
APPEARS IN
संबंधित प्रश्न
Find the surface area of a sphere of radius 5.6 cm.
`["Assume "pi=22/7]`
A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of ₹ 16 per 100 cm2.
`["Assume "pi=22/7]`
A right circular cylinder just encloses a sphere of radius r (see figure). Find
- surface area of the sphere,
- curved surface area of the cylinder,
- ratio of the areas obtained in (i) and (ii).

A model of a ship is made to a scale 1: 300
1) The length of the model of the ship is 2 m. Calculate the lengths of the ship.
2) The area of the deck ship is 180,000 m2. Calculate the area of the deck of the model.
3) The volume of the model in 6.5 m3. Calculate the volume of the ship.
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate:
- the radius of the sphere.
- the number of cones recast. (Take π = `22/7`)
A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast.
A cylinder of same height and radius is placed on the top of a hemisphere. Find the curved
surface area of the shape if the length of the shape be 7 cm.
A hemi-spherical dome of a building needs to be painted. If the circumference of the base of
the dome is 17.6 cm, find the cost of painting it, given the cost of painting is Rs. 5 per l00
`cm^2`
Eight metallic spheres; each of radius 2 mm, are melted and cast into a single sphere. Calculate the radius of the new sphere.
If a hollow sphere of internal and external diameters 4 cm and 8 cm respectively melted into a cone of base diameter 8 cm, then find the height of the cone.
If a sphere is inscribed in a cube, find the ratio of the volume of cube to the volume of the sphere.
A sphere and a cube are of the same height. The ratio of their volumes is
If the ratio of volumes of two spheres is 1 : 8, then the ratio of their surface areas is
If a solid sphere of radius 10 cm is moulded into 8 spherical solid balls of equal radius, then the surface area of each ball (in sq.cm) is
If a sphere is inscribed in a cube, then the ratio of the volume of the sphere to the volume of the cube is
If a solid sphere of radius r is melted and cast into the shape of a solid cone of height r, then the radius of the base of the cone is
A sphere is placed inside a right circular cylinder so as to touch the top, base and lateral surface of the cylinder. If the radius of the sphere is r, then the volume of the cylinder is
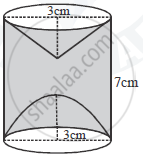
A hemispherical and a conical hole is scooped out of a.solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows:
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm.
Give your answer correct to the nearest whole number.Taken`pi = 22/7`.
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown.
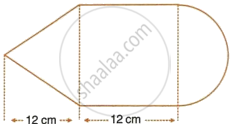
Calculate :
- the total surface area.
- the total volume of the solid and
- the density of the material if its total weight is 1.7 kg.
The radius of two spheres are in the ratio of 1 : 3. Find the ratio between their volume.
