Advertisements
Advertisements
प्रश्न
If a solid sphere of radius 10 cm is moulded into 8 spherical solid balls of equal radius, then the surface area of each ball (in sq.cm) is
विकल्प
100 π
75 π
60 π
50 π
उत्तर
In the given problem, Let the radius of smaller spherical balls which can be made from a bigger ball be xunits.
Here,
The radius of the bigger ball (r1) = 10 cm
The radius of the smaller ball (r2) = x cm
The number of smaller balls = 8
So, volume of the big ball is equal to the volume of 8 small balls.
Volume of the big balls = volume of the 8 small balls
`(4/3)pi r_1^3 = 8 (4/3) pi x^3`
`(4/3) pi (10)^3 =8 (4/3) pi x^3`
`(10)^3 = 8 x^3`
`x^3 = 1000/8`
Further, solving for x, we get,
`x=3sqrt(1000/8) `
`x = 10/2`
x = 5
Now, surface area of a small ball of radius 5 cm = `4 pi r^2`
`= 4 pi(5)^2`
`= 100 pi`
Therefore, the surface area of the small spherical ball is `100 pi`.
APPEARS IN
संबंधित प्रश्न
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres of radius 0.5 cm. Find the number of spheres formed.
Find the surface area of a sphere of radius 10.5 cm .
Find the total surface area of a hemisphere and a solid hemisphere each of radius 10 cm.
(Use 𝜋 = 3.14)
A largest sphere is to be carved out of a right circular cylinder of radius 7 cm and height 14 cm. Find the volume of the sphere.
The cross-section of a tunnel is a square of side 7 m surmounted by a semi-circle as shown in the adjoining figure. The tunnel is 80 m long.
Calculate:
- its volume,
- the surface area of the tunnel (excluding the floor) and
- its floor area.

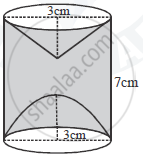
A hemispherical and a conical hole is scooped out of a.solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows:
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm.
Give your answer correct to the nearest whole number.Taken`pi = 22/7`.
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate : the number of cones recast. `("Take" pi =22/7)`
Find the volume and surface area of a sphere of diameter 21 cm.
The radius of two spheres are in the ratio of 1 : 3. Find the ratio between their volume.
A solid sphere is cut into two identical hemispheres.
Statement 1: The total volume of two hemispheres is equal to the volume of the original sphere.
Statement 2: The total surface area of two hemispheres together is equal to the surface area of the original sphere.
Which of the following is valid?
