Advertisements
Advertisements
प्रश्न
If a solid sphere of radius r is melted and cast into the shape of a solid cone of height r, then the radius of the base of the cone is
विकल्प
2r
3r
r
4r
Advertisements
उत्तर
In the given problem, we have a solid sphere which is remolded into a solid cone such that the radius of the sphere is equal to the height of the cone. We need to find the radius of the base of the cone.
Here, radius of the solid sphere (rs) = r cm
Height of the solid cone (h) = r cm
Let the radius of the base of cone (rc) = x cm
So, the volume of cone will be equal to the volume of the solid sphere.
Therefore, we get,
`(1/3) pi r_c^2 h = (4/3) pi r_s^3`
`(1/3) pi x^2 (r) = (4/3) pi (r)^3`
`x^2 = 4r^2`
` x = sqrt(4r^2)`
` x = 2r`
Therefore, radius of the base of the cone is 2r .
APPEARS IN
संबंधित प्रश्न
A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
`["Assume "pi = 22/7]`
A solid cone of radius 5 cm and height 8 cm is melted and made into small spheres of radius 0.5 cm. Find the number of spheres formed.
Find the total surface area of a hemisphere and a solid hemisphere each of radius 10 cm.
(Use 𝜋 = 3.14)
A spherical ball of lead has been melted and made into identical smaller balls with radius equal to half the radius of the original one. How many such balls can be made?
Metallic spheres of radii 6 cm, 8 cm and 10 cm respectively are melted and recasted into a single solid sphere. Taking π = 3.1, find the surface area of the solid sphere formed.
Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r cm.
Spherical marbles of diameter 1.4 cm are dropped into beaker containing some water and are fully submerged. The diameter of the beaker is 7 cm. Find how many marbles have been dropped in it if the water rises by 5.6 cm.
What is the least number of solid metallic spheres, each of 6 cm diameter, that should be melted and recast to form a solid metal cone whose height is 45 cm and diameter 12 cm?
The cross-section of a tunnel is a square of side 7 m surmounted by a semi-circle as shown in the adjoining figure. The tunnel is 80 m long.
Calculate:
- its volume,
- the surface area of the tunnel (excluding the floor) and
- its floor area.
How many spherical bullets can be made out of a solid cube of lead whose edge measures 44 cm, each bullet being 4 cm in diameter?
If a hollow sphere of internal and external diameters 4 cm and 8 cm respectively melted into a cone of base diameter 8 cm, then find the height of the cone.
A sphere and a cube are of the same height. The ratio of their volumes is
If the surface area of a sphere is 144π m2, then its volume (in m3) is
A cone and a hemisphere have equal bases and equal volumes the ratio of their heights is
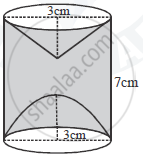
A hemispherical and a conical hole is scooped out of a.solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows:
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm.
Give your answer correct to the nearest whole number.Taken`pi = 22/7`.
Find the length of the wire of diameter 4 m that can be drawn from a solid sphere of radius 9 m.
The volume of a sphere is 905 1/7 cm3, find its diameter.
A vessel is in he form of an inverted cone. Its height is 11 cm., and the radius of its top which is open is 2.5 cm. It is filled with water up to the rim. When lead shots, each of which is a sphere of radius 0.25 cm., are dropped 2 into the vessel, `2/5`th of the water flows out. Find the number of lead shots dropped into the vessel.
