Advertisements
Advertisements
प्रश्न
A right circular cylinder just encloses a sphere of radius r (see figure). Find
- surface area of the sphere,
- curved surface area of the cylinder,
- ratio of the areas obtained in (i) and (ii).

उत्तर
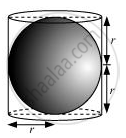
(i) Surface area of sphere = 4πr2
(ii) Height of cylinder = r + r = 2r
The radius of the cylinder = r
The curved surface area of cylinder = 2πrh
= 2πr (2r)
= 4πr2
(iii) Required ratio = `"Surface area of the sphere"/"Curved surface area of cylinder"`
= `(4pir^2)/(4pir^2)= 1/1`
Therefore, the ratio between these two surface areas is 1 : 1.
APPEARS IN
संबंधित प्रश्न
Find the radius of a sphere whose surface area is 154 cm2.
`["Assume "pi=22/7]`
The cross-section of a tunnel is a square of side 7 m surmounted by a semi-circle as shown in the adjoining figure. The tunnel is 80 m long.
Calculate:
- its volume,
- the surface area of the tunnel (excluding the floor) and
- its floor area.

Find the total surface area of a hemisphere of radius 10 cm.
A sphere and a cube are of the same height. The ratio of their volumes is
The ratio between the volume of a sphere and volume of a circumscribing right circular cylinder is
Find the surface area and volume of sphere of the following radius. (π = 3.14 )
9 cm
Find the volume of the hollow sphere whose inner diameter is 8 cm and the thickness of the material of which it is made is 1 cm .
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate : the number of cones recast. `("Take" pi =22/7)`
There is surface area and volume of a sphere equal, find the radius of sphere.
A manufacturing company prepares spherical ball bearings, each of radius 7 mm and mass 4 gm. These ball bearings are packed into boxes. Each box can have maximum of 2156 cm3 of ball bearings. Find the:
- maximum number of ball bearings that each box can have.
- mass of each box of ball bearings in kg.
(use π = `22/7`)
