Advertisements
Advertisements
Question
A right circular cylinder just encloses a sphere of radius r (see figure). Find
- surface area of the sphere,
- curved surface area of the cylinder,
- ratio of the areas obtained in (i) and (ii).

Solution
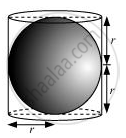
(i) Surface area of sphere = 4πr2
(ii) Height of cylinder = r + r = 2r
The radius of the cylinder = r
The curved surface area of cylinder = 2πrh
= 2πr (2r)
= 4πr2
(iii) Required ratio = `"Surface area of the sphere"/"Curved surface area of cylinder"`
= `(4pir^2)/(4pir^2)= 1/1`
Therefore, the ratio between these two surface areas is 1 : 1.
APPEARS IN
RELATED QUESTIONS
Find the surface area of a sphere of radius 14 cm.
`["Assume "pi=22/7]`
Find the surface area of a sphere of radius 5.6 cm .
A cylinder of same height and radius is placed on the top of a hemisphere. Find the curved
surface area of the shape if the length of the shape be 7 cm.
The diameter of the moon is approximately one fourth of the diameter of the earth. Find the
ratio of their surface areas.
Find the radius of a sphere whose surface area is 154 cm2.
How many spherical bullets can be made out of a solid cube of lead whose edge measures 44 cm, each bullet being 4 cm in diameter?
The largest sphere is cut off from a cube of side 6 cm. The volume of the sphere will be
If the ratio of volumes of two spheres is 1 : 8, then the ratio of their surface areas is
A sphere is placed inside a right circular cylinder so as to touch the top, base and lateral surface of the cylinder. If the radius of the sphere is r, then the volume of the cylinder is
The radius of two spheres are in the ratio of 1 : 3. Find the ratio between their volume.
