Advertisements
Advertisements
Question
The radius of two spheres are in the ratio of 1 : 3. Find the ratio between their volume.
Solution
Let the radius of two sphere number is r1 and r2.
∵ `r_1/r_2 = 1/3`
Volumes of spheres,
V1 = `4/3 πr_1^3`
and V2 = `4/3 πr_2^3`
Now,
`V_1/V_2 = (r_1^3)/(r_2^3) = (r_1/r_2)^3`
`= (1/3)^3 = 1/27`
∴ V1 : V2 = 1: 27
Hence, the volume of two spheres are in the ratio of 1: 27.
APPEARS IN
RELATED QUESTIONS
Find the surface area of a sphere of diameter 21 cm.
`["Assume "pi=22/7]`
Find the surface area of a sphere of radius 5.6 cm .
Find the total surface area of a hemisphere and a solid hemisphere each of radius 10 cm.
(Use 𝜋 = 3.14)
The dome of a building is in the form of a hemisphere. Its radius is 63 dm. Find the cost of
painting it at the rate of Rs. 2 per sq. m.
The volume of a sphere is 38808 cm3; find its diameter and the surface area.
If the number of square centimeters on the surface of a sphere is equal to the number of cubic centimeters in its volume, what is the diameter of the sphere?
Metallic spheres of radii 6 cm, 8 cm and 10 cm respectively are melted and recasted into a single solid sphere. Taking π = 3.1, find the surface area of the solid sphere formed.
If a sphere of radius 2r has the same volume as that of a cone with circular base of radius r, then find the height of the cone.
If the ratio of volumes of two spheres is 1 : 8, then the ratio of their surface areas is
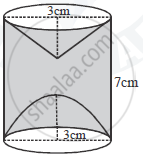
A hemispherical and a conical hole is scooped out of a.solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows:
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm.
Give your answer correct to the nearest whole number.Taken`pi = 22/7`.
The model of a building is constructed with the scale factor 1 : 30.
(i) If the height of the model is 80 cm, find the actual height of the building in meters.
(ii) If the actual volume of a tank at the top of the building is 27m3, find the volume of the tank on the top of the model.
If the surface area of a sphere is 2826 cm2 then find its volume. ( π= 3.14)
Find the volume of a sphere, if its surface area is 154 sq.cm.
A solid metallic cylinder has a radius of 2 cm and is 45 cm tall. Find the number of metallic spheres of diameter 6 cm that can be made by recasting this cylinder .
Find the volume of the hollow sphere whose inner diameter is 8 cm and the thickness of the material of which it is made is 1 cm .
A hemispherical bowl of internal radius 9 cm is full of liquid. This liquid is to be filled into conical shaped small containers each of diameter 3 cm and height 4 cm. How many containers are necessary to empty the bowl?
The total area of a solid metallic sphere is 1256 cm2. It is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate: the number of cones recasted [π = 3.14]
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find: the weight of the material drilled out if it weighs 7 gm per cm3.
A manufacturing company prepares spherical ball bearings, each of radius 7 mm and mass 4 gm. These ball bearings are packed into boxes. Each box can have maximum of 2156 cm3 of ball bearings. Find the:
- maximum number of ball bearings that each box can have.
- mass of each box of ball bearings in kg.
(use π = `22/7`)
