Advertisements
Advertisements
Question
Find the volume of the hollow sphere whose inner diameter is 8 cm and the thickness of the material of which it is made is 1 cm .
Solution
Inner diameter = 8 cm
Inner radius = r = 4 cm
Outer radius = R = 4cm + 1cm thick material = 5 cm
Volume of hemisphere = `2/3pir^3`
Required Volume = `4/3pi(R^3 - r^3)`
= `4/3 xx 22/7 xx (5^3 - 4^3)`
= `4/3 xx 22/7 xx 61`
= 255.6 cm3
Required volume= 255.6 cm3
APPEARS IN
RELATED QUESTIONS
Find the surface area of a sphere of radius 14 cm.
`["Assume "pi=22/7]`
Find the surface area of a sphere of diameter 3.5 m.
`["Assume "pi=22/7]`
Find the surface area of a sphere of radius 14 cm.
The dome of a building is in the form of a hemisphere. Its radius is 63 dm. Find the cost of
painting it at the rate of Rs. 2 per sq. m.
Assuming the earth to be a sphere of radius 6370 km, how many square kilo metres is area
of the land, if three-fourth of the earth’s surface is covered by water?
A hollow sphere of internal and external diameter 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone.
Find the radius of a sphere whose surface area is 154 cm2.
If a hollow sphere of internal and external diameters 4 cm and 8 cm respectively melted into a cone of base diameter 8 cm, then find the height of the cone.
The largest sphere is cut off from a cube of side 6 cm. The volume of the sphere will be
If the ratio of volumes of two spheres is 1 : 8, then the ratio of their surface areas is
Find the surface area and volume of sphere of the following radius. (π = 3.14)
4 cm
Find the surface area of a sphere, if its volume is 38808 cubic cm. `(π = 22/7)`
Find the radius of a sphere whose surface area is equal to the area of the circle of diameter 2.8 cm
How many lead balls of radii 1 cm each can be made from a sphere of 8 cm radius?
From a rectangular solid of metal 42 cm by 30 cm by 20 cm, a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find: the volume of remaining solid
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown.
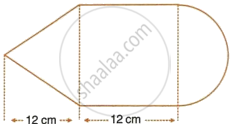
Calculate :
- the total surface area.
- the total volume of the solid and
- the density of the material if its total weight is 1.7 kg.
There is surface area and volume of a sphere equal, find the radius of sphere.
The radius of a sphere increases by 25%. Find the percentage increase in its surface area
A solid sphere is cut into two identical hemispheres.
Statement 1: The total volume of two hemispheres is equal to the volume of the original sphere.
Statement 2: The total surface area of two hemispheres together is equal to the surface area of the original sphere.
Which of the following is valid?
