Advertisements
Advertisements
Question
A hollow sphere of internal and external diameter 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone.
Solution
External diameter = 8 cm
Therefore, radius (R) = 4 cm
Internal diameter = 4 cm
Therefore, radius (r) = 2 cm
Volume of metal used in hollow sphere = `4/3pi(R^3 - r^3)`
= `4/3 xx 22/7 xx (4^3 - 2^3)`
= `88/21(64 - 8)`
= `88/21 xx 56 cm^3` ...(i)
Diameter of cone = 8 cm
Therefore, radius = 4 cm
Let height of cone = h
∴ Volume = `1/3pir^2h`
= `1/3 xx 22/7 xx 4 xx 4 xx h`
= `352/21 h` ...(ii)
From (i) and (ii)
`352/21 h = 88/21 xx 56`
`=> h = (88 xx 56 xx 21)/(21 xx 352) = 14 cm`
Height of the cone = 14 cm.
APPEARS IN
RELATED QUESTIONS
The diameter of the moon is approximately one-fourth of the diameter of the earth. Find the ratio of their surface area.
A certain number of metallic cones, each of radius 2 cm and height 3 cm are melted and recast into a solid sphere of radius 6 cm. Find the number of cones.
A hollow sphere of internal and external radii 6 cm and 8 cm respectively is melted and recast into small cones of base radius 2 cm and height 8 cm. Find the number of cones.
Find the surface area of a sphere of diameter 21 cm .
The dome of a building is in the form of a hemisphere. Its radius is 63 dm. Find the cost of
painting it at the rate of Rs. 2 per sq. m.
The total area of a solid metallic sphere is 1256 cm2. It is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate :
- the radius of the solid sphere.
- the number of cones recast. [Take π = 3.14]
Spherical marbles of diameter 1.4 cm are dropped into beaker containing some water and are fully submerged. The diameter of the beaker is 7 cm. Find how many marbles have been dropped in it if the water rises by 5.6 cm.
The diameter of a sphere is 6 cm. It is melted and drawn into a wire of diameter 0.2 cm. Find the length of the wire.
Find the radius of a sphere whose surface area is 154 cm2.
A sphere is placed inside a right circular cylinder so as to touch the top, base and lateral surface of the cylinder. If the radius of the sphere is r, then the volume of the cylinder is
The model of a building is constructed with the scale factor 1 : 30.
(i) If the height of the model is 80 cm, find the actual height of the building in meters.
(ii) If the actual volume of a tank at the top of the building is 27m3, find the volume of the tank on the top of the model.
Find the surface area and volume of sphere of the following radius. (π = 3.14)
4 cm
If the surface area of a sphere is 2826 cm2 then find its volume. ( π= 3.14)
Find the surface area of a sphere, if its volume is 38808 cubic cm. `(π = 22/7)`
A hemispherical bowl of internal radius 9 cm is full of liquid. This liquid is to be filled into conical shaped small containers each of diameter 3 cm and height 4 cm. How many containers are necessary to empty the bowl?
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown.
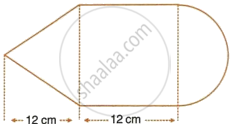
Calculate :
- the total surface area.
- the total volume of the solid and
- the density of the material if its total weight is 1.7 kg.
The volume of a sphere is 905 1/7 cm3, find its diameter.
A sphere cut out from a side of 7 cm cubes. Find the volume of this sphere?
A vessel is in he form of an inverted cone. Its height is 11 cm., and the radius of its top which is open is 2.5 cm. It is filled with water up to the rim. When lead shots, each of which is a sphere of radius 0.25 cm., are dropped 2 into the vessel, `2/5`th of the water flows out. Find the number of lead shots dropped into the vessel.
A manufacturing company prepares spherical ball bearings, each of radius 7 mm and mass 4 gm. These ball bearings are packed into boxes. Each box can have maximum of 2156 cm3 of ball bearings. Find the:
- maximum number of ball bearings that each box can have.
- mass of each box of ball bearings in kg.
(use π = `22/7`)
